
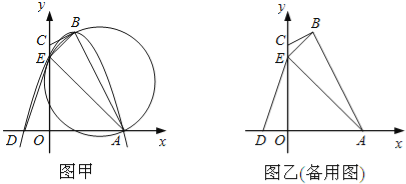
����Ŀ����ͼ�ף��ı���OABC�ı�OA��OC�ֱ���x�ᡢy����������ϣ�������B��������߽�x���ڵ�A��D����y���ڵ�E������AB��AE��BE����֪tan��CBE=![]() ��A��3��0����D����1��0����E��0��3����
��A��3��0����D����1��0����E��0��3����
��1���������ߵĽ���ʽ������B�����ꣻ
��2����֤��CB����ABE���Բ�����ߣ�
��3����̽�����������Ƿ����һ��P��ʹ��D��E��PΪ���������������ABE���ƣ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��4������AOE��x��������ƽ��t����λ���ȣ�0��t��3��ʱ����AOE����ABE�ص����ֵ����Ϊs����s��t֮��ĺ�����ϵʽ����ָ��t��ȡֵ��Χ��
���𰸡���1��y=a��x��3����x+1������B��1��4��
��2��������
��3��������
��4��s=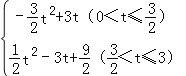
��������
��1�������⣬�������߽���ʽΪy=a��x��3����x+1����
��E��0��3��������ʽ����ã�a=��1��
��y=��x2+2x+3��
���B��1��4����
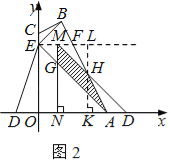
��2��֤������ͼ1������B��BM��y�ڵ�M����M��0��4����
��Rt��AOE��OA=OE=3��
���1=��2=45����AE=![]() =3
=3![]() ��
��
��Rt��EMB��EM=OM��OE=1=BM��
���MEB=��MBE=45����BE=![]() =
=![]() ��
��
���BEA=180�㩁��1����MEB=90����
��AB����ABE���Բ��ֱ����
��Rt��ABE��tan��BAE=![]() =
=![]() =tan��CBE��
=tan��CBE��
���BAE=��CBE��
��Rt��ABE����BAE+��3=90�������CBE+��3=90����
���CBA=90������CB��AB��
��CB����ABE���Բ�����ߣ�
��3���⣺Rt��ABE�У���AEB=90����tan��BAE=![]() ��sin��BAE=
��sin��BAE=![]() ��cos��BAE=
��cos��BAE=![]() ��
��
����D��E��PΪ���������������ABE���ƣ�����DEP��Ϊֱ�������Σ�
��DEΪб��ʱ��P1��x���ϣ���ʱP1��O�غϣ�
��D����1��0����E��0��3������OD=1��OE=3����tan��DEO=![]() =tan��BAE������DEO=��BAE
=tan��BAE������DEO=��BAE
������DEO�ס�BAE����������� O���Ƿ���������P1�㣬����Ϊ��0��0����
��DEΪ��ֱ�DZ�ʱ��P2��x���ϣ�
����D��E��PΪ���������������ABE���ƣ�����DEP2=��AEB=90����sin��DP2E=sin��BAE=![]() ��
��
��DE=![]() =
=![]() ����DP2=DE��sin��DP2E=
����DP2=DE��sin��DP2E=![]() ��
��![]() =10��OP2=DP2��OD=9
=10��OP2=DP2��OD=9
����P2��9��0����
��DEΪ��ֱ�DZ�ʱ����P3��y���ϣ�
����D��E��PΪ���������������ABE���ƣ�����EDP3=��AEB=90����cos��DEP3=cos��BAE=![]() ��
��
��EP3=DE��cos��DEP3=![]() ��
��![]() =
=![]() ��OP3=EP3��OE=
��OP3=EP3��OE=![]() ��
��
���ϣ��ã�P1��0��0����P2��9��0����P3��0����![]() ����
����
��4���⣺��ֱ��AB�Ľ���ʽΪy=kx+b��
��A��3��0����B��1��4�����룬��![]() ���
���![]()
��y=��2x+6��
����E������EF��x�ύAB�ڵ�F����y=3ʱ����x=![]() ����F��
����F��![]() ��3����
��3����
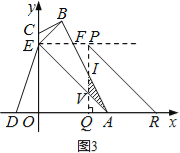
���һ����ͼ2����0��t��![]() ʱ������AOEƽ�Ƶ���DNM��λ�ã�MD��AB�ڵ�H��MN��AE�ڵ�G��
ʱ������AOEƽ�Ƶ���DNM��λ�ã�MD��AB�ڵ�H��MN��AE�ڵ�G��
��ON=AD=t������H��LK��x���ڵ�K����EF�ڵ�L��
����AHD�ס�FHM����![]() ����
����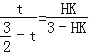 ��
��
���HK=2t��
��S��=S��MND��S��GNA��S��HAD=![]() ��3��3��
��3��3��![]() ��3��t��2��
��3��t��2��![]() t2t=��
t2t=��![]() t2+3t��
t2+3t��
���������ͼ3����![]() ��t��3ʱ������AOEƽ�Ƶ���PQR��λ�ã�PQ��AB�ڵ�I����AE�ڵ�V��
��t��3ʱ������AOEƽ�Ƶ���PQR��λ�ã�PQ��AB�ڵ�I����AE�ڵ�V��
����IQA�ס�IPF����![]() ����
����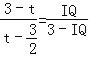 ��
��
���IQ=2��3��t����
��S��=S��IQA��S��VQA=![]() ����3��t����2��3��t����
����3��t����2��3��t����![]() ��3��t��2=
��3��t��2=![]() ��3��t��2=
��3��t��2=![]() t2��3t+
t2��3t+![]() ��
��
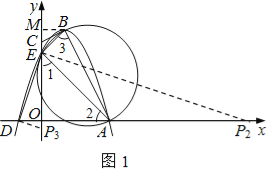
����������s=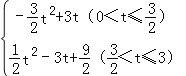 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
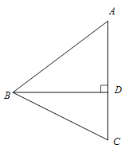
����Ŀ����ͼ������ABC�У�AB=AC>BC��BD ��AC���ϵĸߣ���C����ֱ��BD�ĶԳƵ�Ϊ��E������BE.
(1)�������ⲹȫͼ�Σ�
������BAC=![]() �����DBE�Ĵ�С���ú�
�����DBE�Ĵ�С���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
(2)��DE=2AE����F��BE�е㣬����AF��BD=4����AF�ij�.
 ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC=m��PΪBC������һ�㣬��PA2+PBPC��ֵΪ��������
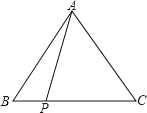
A. m2 B. m2+1 C. 2m2 D. ��m+1��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
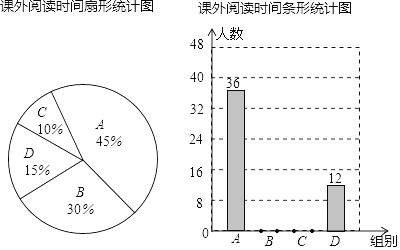
����Ŀ��Ϊ�˴�������У����ʵ����ѧ������飬�����飮ij��ѧ��չ�ˡ�������ҳɳ����Ķ���ڻ��Ϊ���˽ⱾУѧ��ÿ�ܿ����Ķ�ʱ�䣬�����ȡ����ѧ�������ʾ����飬�������Ķ�ʱ���ΪA��B��C��D���飬�����ó������õ����ݻ���������ͳ��ͼ��
��� | �����Ķ�t����λ��ʱ�� |
A | X��2 |
B | 2��x��3 |
C | 3��x��4 |
D | x��4 |
�����ͼ���ṩ����Ϣ������������⣺
��1��һ��������________��ѧ����
��2������ͳ��ͼ��A���Բ�ĽǶ���________��
��3��ֱ�Ӳ�ȫ����ͳ��ͼ
��4������У��2400��ѧ����������������Ľ��������ÿ�ܿ����Ķ�ʱ�䲻��3Сʱ��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
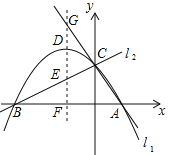
����Ŀ����2017�Ĵ�ʡ�����У���31�⣬12�֣���ͼ����֪��ֱ��l1��l2�ֱ���A��1��0������B����3��0����������ֱ���ཻ��y����������ϵĵ�C������C������Ϊ��0��![]() ��ʱ��ǡ����l1��l2��������A��B��C�������ߵĶԳ�����l1��l2��x��ֱ��ڵ�G��E��F��DΪ�����ߵĶ��㣮
��ʱ��ǡ����l1��l2��������A��B��C�������ߵĶԳ�����l1��l2��x��ֱ��ڵ�G��E��F��DΪ�����ߵĶ��㣮
��1���������ߵĺ�������ʽ��
��2����˵��DG��DE��������ϵ����˵�����ɣ�
��3����ֱ��l2�Ƶ�C��תʱ���������ߵ���һ������ΪM������MCGΪ����������ʱ����ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ͼ�е�MA1��NAnƽ�У�
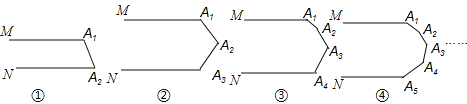
��1��ͼ���е���A1+��A2= �ȣ�ͼ���е���A1+��A2+��A3= �ȣ�
ͼ���е���A1+��A2+��A3+��A4= �ȣ�ͼ���е���A1+��A2+��A3+��A4+��A5= �ȣ�����
�ڢ��ͼ�е���A1+��A2+��A3+��+��A10= ��
��2����n��ͼ�е���A1+��A2+��A3+��+��An= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����¿�����һ�ֵ綯����ͼ�����Ĵ��A����Ĺ���AB��AC�����MN���е���Ƿֱ�Ϊ8���10�㣬���A����������ľ���Ϊ1m��ó������������Ŀ���BC�����������������أ����������ݣ�sin8��=![]() ��tan8��=
��tan8��=![]() ��sin10��=
��sin10��=![]() ��tan10��=
��tan10��=![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
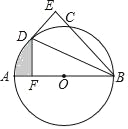
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ABC��ƽ���߽���O�ڵ�D��DE��BC�ڵ�E��
��1�����ж�DE���O��λ�ù�ϵ����˵�����ɣ�
��2������D��DF��AB�ڵ�F����BE=3![]() ��DF=3����ͼ����Ӱ���ֵ������
��DF=3����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ�����
��ͼ���ϣ�����![]() ��
��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() .
.

��1����������![]() ��һ�κ���
��һ�κ���![]() �ı���ʽ��
�ı���ʽ��
��2��ֱ��д������![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com