
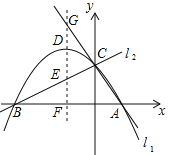
【题目】(2017四川省巴中市,第31题,12分)如图,已知两直线l1,l2分别经过点A(1,0),点B(﹣3,0),且两条直线相交于y轴的正半轴上的点C,当点C的坐标为(0,![]() )时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与l1、l2、x轴分别交于点G、E、F,D为抛物线的顶点.
)时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与l1、l2、x轴分别交于点G、E、F,D为抛物线的顶点.
(1)求抛物线的函数解析式;
(2)试说明DG与DE的数量关系?并说明理由;
(3)若直线l2绕点C旋转时,与抛物线的另一个交点为M,当△MCG为等腰三角形时,请直接写出点M的坐标.
【答案】(1)![]() ;(2)DG=DE;(3)(﹣2,
;(2)DG=DE;(3)(﹣2,![]() ),(﹣1,
),(﹣1,![]() ).
).
【解析】试题(1)设抛物线的函数解析式为![]() .将点A、B、C的坐标代入,得到关于a、b、c的方程组,解方程求出a、b、c的值,进而得到抛物线的解析式;
.将点A、B、C的坐标代入,得到关于a、b、c的方程组,解方程求出a、b、c的值,进而得到抛物线的解析式;
(2)利用待定系数法分别求出直线l1、直线l2的解析式,再求出G、D、E的坐标,计算得出DG的长;
(3)当△MCG为等腰三角形时,分三种情况:①GM=GC;②CM=CG;③MC=MG.
试题解析:解:(1)设抛物线的函数解析式为![]() .
.
∵点A(1,0),点B(﹣3,0),点C(0,![]() )在抛物线上,∴
)在抛物线上,∴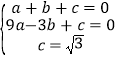 ,解得:
,解得: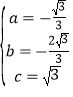 ,∴抛物线的函数解析式为
,∴抛物线的函数解析式为![]() ;
;
(2)DG=DE.理由如下:
设直线l1的解析式为y=k1x+b1,将A(1,0),C(0,![]() )代入,解得
)代入,解得![]() ;
;
设直线l2的解析式为y=k2x+b2,将B(﹣3,0),C(0,![]() )代入,解得
)代入,解得![]() ;
;
∵抛物线与x轴的交点为A(1,0),B(﹣3,0),∴抛物线的对称轴为直线x=﹣1,又∵点G、D、E均在对称轴上,∴G(﹣1,![]() ),D(﹣1,
),D(﹣1,![]() ),E(﹣1,
),E(﹣1,![]() ),∴DG=
),∴DG=![]() ﹣
﹣![]() =
=![]() ,DE=
,DE=![]() ﹣
﹣![]() =
=![]() ,∴DG=DE;
,∴DG=DE;
(3)若直线l2绕点C旋转时,与抛物线的另一个交点为M,当△MCG为等腰三角形时,分三种情况:
①以G为圆心,GC为半径画弧交抛物线于点M1、C,点M1与C关于抛物线的对称轴对称,则M1的坐标为(﹣2,![]() );
);
②以C为圆心,GC为半径画弧交抛物线于点M2、M3,点M2与点A重合,点A、C、G在一条直线上,不能构成三角形,M3与M1重合;
③作线段GC的垂直平分线,交抛物线于点M4、M5,点M4与点D重合,点D的坐标为(﹣1,![]() ),M5与M1重合;
),M5与M1重合;
综上所述:满足条件的点M只有两个,其坐标分别为(﹣2,![]() ),(﹣1,
),(﹣1,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
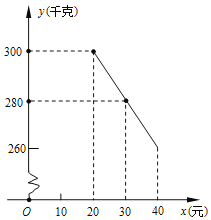
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x 的函数关系图象.
(1)求y与x的函数关系式;
(2)直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
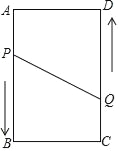
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
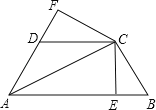
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)若AB=15,AD=7,BC=5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
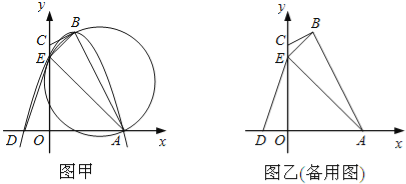
【题目】如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)![]() ,其中
,其中![]()
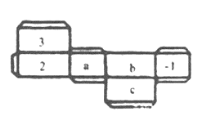
(2)如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
①填空:![]() _________,
_________,![]() _________
_________![]() _________;
_________;
②先化简,再求值:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平行四边形ABCD,求作菱形AECF,使点E、点F分别在BC、AD边上
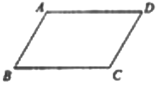
下面是小明设计的尺规作图过程.
作法:如图
① 连接AC;
② 分别以A、C为圆心,大于![]() AC的长为半径作弧,两弧交于M、N两点;
AC的长为半径作弧,两弧交于M、N两点;
③ 连接MN,分别与BC、AD、AC交于E、F、O三点;
④ 连接AE、CF
四边形AECF即为所求
根据小明设计的尺规作图过程
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明
证明∵AM= ,AN= ,
∴MN是AC的垂直平分线。
( )(填推理的依据)
∴EF⊥AC,OA=OC,
∴平行四边形ABCD
∴AD∥BC
∴∠FAO=∠ECO
在△FAO和△ECO中

∴△FAO≌△ECO
∴OE=OF
又∵OA=OC
∴四边形AECF是平行四边形
( )(填推理依据)
∵EF⊥AC
∴四边形AECF是菱形
( )(填推理依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线,便把正方形分成
条横线,便把正方形分成![]() 部分(如图①);如果在正方形中画
部分(如图①);如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线,便把正方形分成
条横线,便把正方形分成![]() 部分(如图②);如果在正方形中画
部分(如图②);如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线,便把正方形分成
条横线,便把正方形分成![]() 部分(如图③...如果在正方形中画
部分(如图③...如果在正方形中画![]() 条纵线和
条纵线和![]() 条横线.便把正方形分成( )部分
条横线.便把正方形分成( )部分

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com