
【题目】如图,△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,连接A2B1并延长到点B2 , 使A2B1=B1B2 , 以A2B2为边作等边△A2B2C2 , A3为等边△A2B2C2的中心,连接A3B2并延长到点B3 , 使A3B2=B2B3 , 以A3B3为边作等边△A3B3C3 , 依次作下去得到等边△AnBnCn , 则等边△A6B6C6的边长为 . 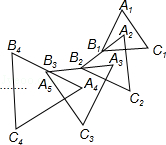
【答案】![]()
【解析】解:作A2D1⊥A1B1于D1 , A3D2⊥A2B2于D2 , 如图, ∵△A1B1C1是边长为1的等边三角形,A2为等边△A1B1C1的中心,
∴∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,
,
∴cos∠A2B1D1=cos30°= ![]() =
= ![]() ,
,
∴A2B1= ![]() ,
,
∵A2B1=B1B2 ,
∴A2B2= ![]() ,
,
同理可得∠A3B2D2=30°,B2D2= ![]() A2B2=
A2B2= ![]() ×
× ![]() =
= ![]() ,
,
∴cos∠A3B2D2=cos30°= ![]() =
= ![]() ,
,
∴A3B2= ![]() ,
,
∵A3B2=B2B3 ,
∴A3B3= ![]() =(
=( ![]() )2 ,
)2 ,
同理可得A4B4=( ![]() )3 ,
)3 ,
A5B5=( ![]() )4 . A6B6C=(
)4 . A6B6C=( ![]() )5=
)5= ![]() ,
,
故答案为 ![]() .
.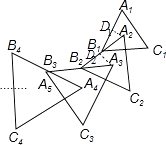
作A2D1⊥A1B1于D1 , A3D2⊥A2B2于D2 , 根据等边三角形的中心的性质得∠A2B1D1=30°,B1D1= ![]() A1B1=
A1B1= ![]() ,利用余弦的定义得cos∠A2B1D1=cos30°=
,利用余弦的定义得cos∠A2B1D1=cos30°= ![]() =
= ![]() ,可计算出A2B1=
,可计算出A2B1= ![]() ,由A2B1=B1B2得到A2B2=
,由A2B1=B1B2得到A2B2= ![]() ,用同样的方法可计算出A3B3=(
,用同样的方法可计算出A3B3=( ![]() )2 , 特殊的结论.
)2 , 特殊的结论.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: ①a﹣b+c>0;
②3a+b=0;
③b2=4a(c﹣n);
④一元二次方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中正确结论的个数是( )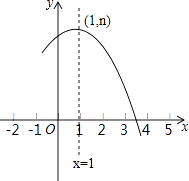
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.
(1)求出该品牌应急灯、手电筒的定价分别是多少元?
(2)经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误是( )
A.众数是85
B.平均数是85
C.方差是20
D.极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠ACD是△ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG∥CE,交AB于点G,若∠1=70°,∠2=30°,则∠3的度数为( )

A. 30° B. 40° C. 45° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB边的垂直平分线![]() 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线![]() 交BC于E,
交BC于E, ![]() 与
与![]() 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
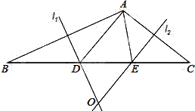
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”问题:小溪边长着两棵棕榈树,恰好隔岸相望一棵棕榈树高是30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺;两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以相同的速度飞去抓鱼,并且同时到达目标.问:这条鱼出现的地方离比较高的棕榈树的树根有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 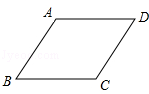
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com