
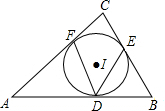
 如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°.
如图:⊙I内切于△ABC,切点分别为D、E、F,若∠A=50°,∠B=60°,连接DE,DE,则∠EDF=55°. 科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图,AD是△ABC的中线.
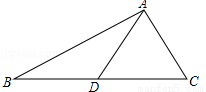
(1)画图:延长AD到E,使ED=AD,连接BE、CE;
(2)四边形ABEC是平行四边形吗?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
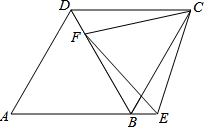 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
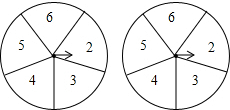 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,□ABCD绕点A逆时针旋转32°,得到□AB′C′D′,若点B′与点B是对应点,若点B′恰好落在BC边上,则∠C=( )
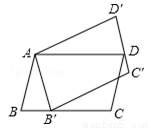
A. 106° B. 146° C. 148° D. 156°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com