练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下面的方格图是由边长为1的若干个小正方形拼成的，ABC的顶点A，B，C均在小正方形的顶点上．

    （1）在图中建立恰当的平面直角坐标系，取小正方形的边长为一个单位长度，且使点A的坐标为（﹣4，2）；

    （2）在（1）中建立的平面直角坐标系内画出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1各顶点的坐标．

    【答案】（1）见解析；（2）见解析，A1（4，2），B1（1，2），C1（2，5）．

    【解析】

    试题分析：（1）根据点A的坐标为（﹣4，2）建立坐标系即可；

    （2）作出各点关于y轴的对称点，再顺次连接，写出三角形各顶点的坐标即可．

    解：（1）如图所示；

    （2）如图所示，A1（4，2），B1（1，2），C1（2，5）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，点P从A出发沿AC向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒．

    （1）当t=2时，求线段PQ的长度；

    （2）当t为何值时，△PCQ的面积等于5cm2？

    （3）在P、Q运动过程中，在某一时刻，若将△PQC翻折，得到△EPQ，如图2，PE与AB能否垂直？若能，求出相应的t值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，∠C=90°，∠B=30°．

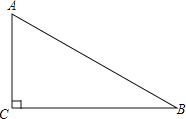
    （1）用直尺和圆规在BC上找一点D，使DA=DB．（不写作法，保留作图痕迹）

    （2）若BC=8，求点D到边AB的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】居民区内的“广场舞”引起媒体关注，辽宁都市频道为此进行过专访报道．小平想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：A 非常赞同；B 赞同但要有时间限制；C 无所谓；D 不赞同．并将调查结果绘制了图1和图2两幅不完整的统计图．

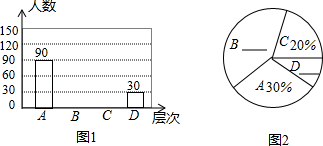
    请你根据图中提供的信息解答下列问题：

    （1）求本次被抽查的居民有多少人？

    （2）将图1和图2补充完整；

    （3）求图2中“C”层次所在扇形的圆心角的度数；

    （4）估计该小区4000名居民中对“广场舞”的看法表示赞同（包括A层次和B层次）的大约有多少人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的解题过程：

    解方程：|x+3|=2．

    解：当x+3≥0时，原方程可化成为x+3=2

    解得x=-1，经检验x=-1是方程的解；

    当x+3＜0，原方程可化为，-（x+3）=2

    解得x=-5，经检验x=-5是方程的解．

    所以原方程的解是x=-1，x=-5．

    解答下面的两个问题：

    （1）解方程：|3x-2|-4=0；

    探究：当值a为何值时，方程|x-2|=a， ①无解；②只有一个解；③有两个解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O为直线AB上一点，∠AOC=58°，OD平分∠AOC，∠DOE=90°．

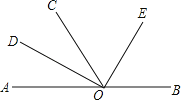
    （1）求出∠BOD的度数；

    （2）请通过计算说明：OE是否平分∠BOC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线的顶点D的坐标为（1，﹣4），与y轴交于点C（0，﹣3），与x轴交于A、B两点．

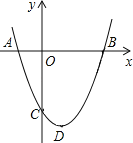
    （1）求该抛物线的函数关系式；

    （2）在抛物线上存在点P（不与点D重合），使得S△PAB=S△ABD，请求出P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y=﹣2x+8与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．

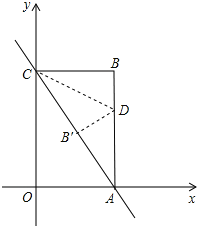
    （1）求点A、C的坐标；

    （2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式；

    （3）在（2）的条件下，坐标平面内是否存在点P（除点B外），使得△APC与△ABC全等？若存在，直接写出符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】温州一位老人制作的仿真郑和宝船尺寸如图，已知在某一直角坐标系中，点A坐标为（9，0）．

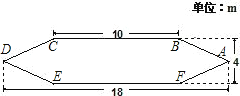
    （1）请你直接在图中画出该坐标系；

    （2）写出其余5点的坐标；

    （3）仿真郑和宝船图中互相平行的线段有哪些？分别写出来．

    查看答案和解析>>

    同步练习册答案