
����Ŀ���������ڵġ��㳡�衱����ý���ע����������Ƶ��Ϊ�˽��й�ר�ñ�����Сƽ���˽ⱾС������ԡ��㳡�衱�Ŀ�����������һ�γ������飬�Ѿ���ԡ��㳡�衱�Ŀ�����Ϊ�ĸ���Σ�A �dz���ͬ��B ��ͬ��Ҫ��ʱ�����ƣ�C ����ν��D ����ͬ������������������ͼ1��ͼ2������������ͳ��ͼ��
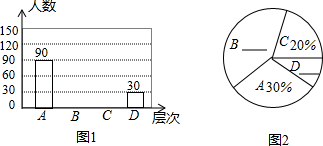
�������ͼ���ṩ����Ϣ����������⣺
��1���α����ľ����ж����ˣ�
��2����ͼ1��ͼ2����������
��3����ͼ2�С�C������������ε�Բ�ĽǵĶ�����
��4�����Ƹ�С��4000�������жԡ��㳡�衱�Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ�ж����ˣ�
���𰸡���1�����α����ľ�����300�ˣ���2������������3����C������������ε�Բ�ĽǵĶ���Ϊ72�㣻��4�����Ƹ�С��4000�������жԡ��㳡�衱�Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��2800�ˣ�
��������
�����������1����A��ε�����������ռ�İٷֱ���������ѧ���������ɣ�
��2����D��������������������D��ռ�İٷֱȣ������B��ռ�İٷֱȣ��ٳ����������ɵ�B���������������������C�����ռ�İٷֱȿɵ�C��ε�������ȫͼ�μ��ɣ�
��3����360�����C��ε�������ռ�İٷֱȼ��ɵá�C������������ε�Բ�ĽǵĶ�����
��4�����������A�����B��εİٷֱ�֮�ͣ�����4000���ɵõ������
�⣺��1��90��30%=300���ˣ���
�𣺱��α����ľ�����300�ˣ�
��2��D��ռ�İٷֱȣ�30��300=10%
B��ռ�İٷֱȣ�1��20%��30%��10%=40%��
B��Ӧ��������300��40%=120���ˣ���
C��Ӧ��������300��20%=60���ˣ���
��ȫͳ��ͼ����ͼ��ʾ��
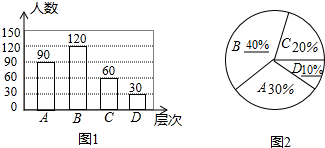
��3��360���20%=72�㣬
�𣺡�C������������ε�Բ�ĽǵĶ���Ϊ72�㣻
��4��4000����30%+40%��=2800���ˣ���
�𣺹��Ƹ�С��4000�������жԡ��㳡�衱�Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��2800�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�۸�aԪ������10%���ֽ���10%�����۶��������̵���������20%����ۺ����ֲ�Ʒ�۸�Ϊ�� ��
A.aԪ
B.1.08aԪ
C.0.972aԪ
D.0.96aԪ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.�ӳ�����OA����B
B.�߶�ABΪֱ��AB��һ����
C.��һ��ֱ�ߣ�ʹ���ij���Ϊ3cm
D.����AB������BA��ͬһ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���ǣ� ��
A��a+2b=3ab B��3a2��2a2=1
C��a2a4=a8 D������a2b��3�£�a3b��2=��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ķ���ͼ���ɱ߳�Ϊ1�����ɸ�С������ƴ�ɵģ�ABC�Ķ���A��B��C����С�����εĶ����ϣ�
��1����ͼ�н���ǡ����ƽ��ֱ������ϵ��ȡС�����εı߳�Ϊһ����λ���ȣ���ʹ��A������Ϊ����4��2����
��2���ڣ�1���н�����ƽ��ֱ������ϵ�ڻ�����ABC����y��ԳƵ���A1B1C1����д����A1B1C1����������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������������飬������25�ˣ�������17�ˣ����������x�˵����飬��ô���������ǡ��������������2��������������г����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����֧���̶Ӹ�10����Ա�����ߣ���λ��cm�����±���

��1���Ӷ�Ա��ƽ������Ϊ cm���ҶӶ�Ա��ƽ������Ϊ cm��
��2��������ѧ����ͳ��֪ʶ�ж���֧���̶ӵ����߸�Ϊ�����أ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com