练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点P（3，1）关于x轴的对称点P′的坐标是_________.

    【答案】（3，-1）

    【解析】∵关于x轴对称的点，横坐标相同，纵坐标互为相反数

    ∴点P（3，1）关于x轴的对称点P′的坐标为（3，-1）.

    故答案为：（3，-1）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

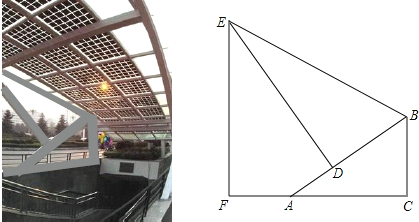
    【题目】如图是某地下商业街的入口，数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF．经测量，支架的立柱BC与地面垂直，即∠BCA=90°，且BC=1.5m，点F、A、C在同一条水平线上，斜杆AB与水平线AC的夹角∠BAC=30°，支撑杆DE⊥AB于点D，该支架的边BE与AB的夹角∠EBD=60°，又测得AD=1m．请你求出该支架的边BE及顶端E到地面的距离EF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，点P从A出发沿AC向C点以1厘米/秒的速度匀速移动；点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动．点P、Q分别从起点同时出发，移动到某一位置时所需时间为t秒．

    （1）当t=2时，求线段PQ的长度；

    （2）当t为何值时，△PCQ的面积等于5cm2？

    （3）在P、Q运动过程中，在某一时刻，若将△PQC翻折，得到△EPQ，如图2，PE与AB能否垂直？若能，求出相应的t值；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6）．

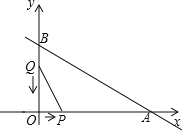
    （1）设△POQ的面积为s，写出s关于t的函数关系式；当t为何值时，△POQ的面积最大，这时面积是多少

    （2）当t为何值时，△POQ与△AOB相似？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，AD⊥BC于D，若AB=4cm，AD=2cm，E为AB的中点，P为AD上一点，PE+PB的最小值为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

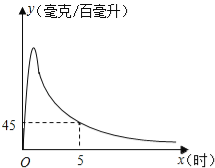
    【题目】实验数据显示，一般成人喝半斤低度白酒后，1.5小时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=﹣200x2+400x刻画；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=（k＞0）刻画（如图所示）．

    （1）根据上述数学模型计算：

    ①喝酒后几时血液中的酒精含量达到最大值？最大值为多少？

    ②当x=5时，y=45，求k的值．

    （2）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，∠C=90°，∠B=30°．

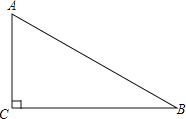
    （1）用直尺和圆规在BC上找一点D，使DA=DB．（不写作法，保留作图痕迹）

    （2）若BC=8，求点D到边AB的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】居民区内的“广场舞”引起媒体关注，辽宁都市频道为此进行过专访报道．小平想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：A 非常赞同；B 赞同但要有时间限制；C 无所谓；D 不赞同．并将调查结果绘制了图1和图2两幅不完整的统计图．

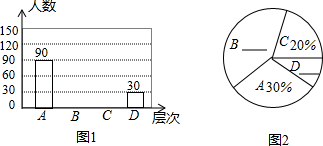
    请你根据图中提供的信息解答下列问题：

    （1）求本次被抽查的居民有多少人？

    （2）将图1和图2补充完整；

    （3）求图2中“C”层次所在扇形的圆心角的度数；

    （4）估计该小区4000名居民中对“广场舞”的看法表示赞同（包括A层次和B层次）的大约有多少人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线y=﹣2x+8与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．

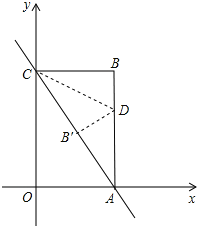
    （1）求点A、C的坐标；

    （2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式；

    （3）在（2）的条件下，坐标平面内是否存在点P（除点B外），使得△APC与△ABC全等？若存在，直接写出符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案