
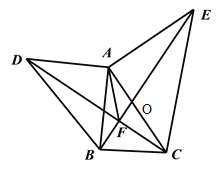
【题目】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE。连结DC、BE交于F点。

(1)求证:△DAC≌△BAE;
(2)求证:DC⊥BE;
(3)求证:∠DFA=∠EFA.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)由题意可得AD=AB,AC=AE,由∠DAB=∠CAE=90°,可得到∠DAC=∠BAE,从而可证△DAC≌△BAE;
(2)由(1)可得∠ACD=∠AEB,再利用直角三角形的性质及等量代换即可得到结论;
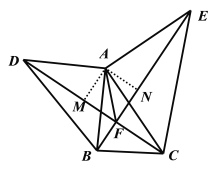
(3)作AM⊥DC于M,AN⊥BE于N,利用全等三角形的面积相等及角平分线的判定即可证得结论.
证明:(1)∵![]()
![]() ,
,
∴![]() ,
,
即![]() ,
,
又∵![]() ,AC=AE,
,AC=AE,
∴△DAC≌△BAE;
(2)∵△DAC≌△BAE,
∴∠ACD=∠AEB,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() ≌
≌![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的平分线,
的平分线,
即![]() .
.
故答案为:(1)证明见解析;(2)证明见解析;(3)证明见解析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】近年来,《政府工作报告》中不断提出了很多新的词汇,为了解学生们对新词汇的关注度,某数学兴趣小组选取其中的![]() :“互联网+政务服务”,
:“互联网+政务服务”,![]() :“工匠精神”,
:“工匠精神”,![]() :“光网城市”,
:“光网城市”,![]() :“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图:请根据统计图提供的信息,解答下列问题:
:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图:请根据统计图提供的信息,解答下列问题:


(1)本次一共调查了多少名同学?
(2)求出统计图中![]() ,
,![]() 的值;
的值;
(3)扇形统计图中,热词![]() 、
、![]() 所在扇形统计图的圆心角分别是多少度?
所在扇形统计图的圆心角分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法:(2x+a)(3x+b),由于甲抄错了第一个多项式中a的符号,得到的结果为6x2+11x-10;由于乙漏抄了第二个多项式中的x的系数,得到的结果为2x2-9x+10.请你计算出a,b的值各是多少,并写出这道整式乘法的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点。

⑴ 填空:AD=CD=_____ .
⑵ 过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
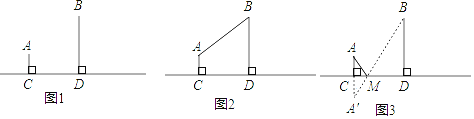
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选
方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)
方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q在CD中间,DQ为多少时?△ABQ为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
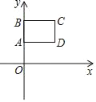
【题目】如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)顶点B的坐标为 ,顶点D的坐标为 (用a或b表示);
(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;
(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度,再向下平移 个单位长度的两次平移;
②若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从广州去某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
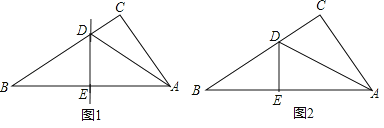
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com