
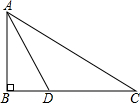
 如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)
如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)  小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )
如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.
中国“蛟龙”号深潜器目前最大测潜极限为7062.68米,某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA查看答案和解析>>
科目:初中数学 来源: 题型:选择题
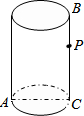 如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点且PC=$\frac{2}{3}$BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )| A. | (4+$\frac{6}{π}$)cm | B. | 5cm | C. | 2$\sqrt{13}$cm | D. | 7cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a3+a3=3a6 | B. | (-a)2•a3=-a6 | C. | (-$\frac{1}{2}$)-2=4 | D. | (-2)0=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com