
 我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA
我们知道,直角三角形的边角关系可用三角函数来描述,那么在任意三角形中,边角之间是否也存在某种关系呢?如图,锐角△ABC中,点A、B、C所对的边分别为a、b、c,过点C作CD⊥AB,在Rt△ADC中,CD=bsinA,AD=bcosA分析 (1)根据给出的公式,把已知条件代入计算,求出a的值,根据勾股定理的逆定理证明直角三角形,根据等腰直角三角形的性质即可得到答案;
(2)把数据代入相应的公式,得到关于c的一元二次方程,解方程得到答案.
解答 解:(1)在锐角△ABC中,a2=b2+c2-2bccosA
=(2$\sqrt{2}$)2+4-2×2$\sqrt{2}$×2×$\frac{\sqrt{2}}{2}$
=4
解得,a=2,
22+22=(2$\sqrt{2}$)2
∴△ABC为直角三角形,a=c=2,
∴∠C=45°;
(2)∵b2=a2+c2-2accosB,
∴c2-$\sqrt{6}$c+1=0,
解得,c=$\frac{\sqrt{6}±\sqrt{2}}{2}$,
∵c>a>b,
∴c=$\frac{\sqrt{6}+\sqrt{2}}{2}$.
点评 本题考查的是新定义和解直角三角形的知识,理解新定义并正确运用新定义的公式是解题的关键,注意应熟记特殊角的三角函数值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
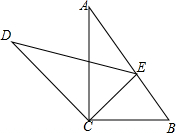 如图,直角三角形ABC中,∠ACB=90°,将△ABC绕点C按逆时针方向旋转α后得到△DEC,此时点E在AB边上,则∠A的度数是$\frac{1}{2}α$(用含α的代数式表示)
如图,直角三角形ABC中,∠ACB=90°,将△ABC绕点C按逆时针方向旋转α后得到△DEC,此时点E在AB边上,则∠A的度数是$\frac{1}{2}α$(用含α的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
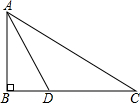 如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)
如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知BD平分∠ABF,且交AE于点D,
如图,已知BD平分∠ABF,且交AE于点D,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com