
【题目】如图,直线y=x+3与两坐标轴交于A,B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)直接写出A、B两点的坐标;
(2)求抛物线的解析式和顶点D的坐标;
(3)在抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.

【答案】(1)B(0,3),A(﹣3,0);(2)抛物线解析式为:y=﹣x2﹣2x+3;顶点D坐标为(﹣1,4);(3)存在,符合条件的点P的坐标为(﹣1,4)或(2,﹣5).
【解析】试题分析:(1)分别令x=0和y=0代入y=x+3中可得结论;
(2)利用待定系数法求二次函数的解析式,根据配方法可得顶点D的坐标;
(3)分两种情况:设点P的坐标为(t,﹣t2﹣2t+3).根据两点距离公式可得:AB2=32+32=18,AP2=(t+3)2+(﹣t2﹣2t+3)2,BP2=t2+(﹣t2﹣2t)2.
①如图1,如果点B为直角顶点,那么AB2+BP2=AP2;
②如图2,如果点A为直角顶点,那么AP2+AB2=BP2,列方程可得结论.
试题解析:解:(1)当x=0时,y=3,∴B(0,3),当y=0时,x+3=0,x=﹣3,∴A(﹣3,0);
(2)把A(﹣3,0),B(0,3)分别代入y=﹣x2+bx+c得:
![]() ,解得:
,解得: ![]() ,∴抛物线解析式为:y=﹣x2﹣2x+3;
,∴抛物线解析式为:y=﹣x2﹣2x+3;
顶点D坐标为(﹣1,4)
(3)存在.
设点P的坐标为(t,﹣t2﹣2t+3).
∵A(﹣3,0),B(0,3),∴AB2=32+32=18,AP2=(t+3)2+(﹣t2﹣2t+3)2,BP2=t2+(﹣t2﹣2t)2.
当△PAB是以AB为直角边的直角三角形时,可分两种情况:
①如图1,如果点B为直角顶点,那么AB2+BP2=AP2
(事实这里的点P与点D 重合)
即18+t2+(﹣t2﹣2t)2=(t+3)2+(﹣t2﹣2t+3)2,整理得t2+t=0,解得t1=﹣1,t2=0(不合题意舍去),则点P的坐标为(﹣1,4);
②如图2,如果点A为直角顶点,那么AP2+AB2=BP2,即18+(t+3)2+(﹣t2﹣2t+3)2=t2+(﹣t2﹣2t)2,整理得t2+t﹣6=0,解得t1=2,t2=﹣3(不合题意舍去),则点P的坐标为(2,﹣5);
综上所述:所有符合条件的点P的坐标为(﹣1,4)或(2,﹣5).
另解:如图3,作DE⊥y轴于点E,发现∠ABO=∠DBE=45°
可知顶点D满足△DAB是直角三角形,这时点P的坐标为(﹣1,4);
作PA⊥AB交抛物线于点P,作PF⊥x轴于点F,发现∠PAF=∠APF=45°,由PF=AF求出另一点P为(2,﹣5).



科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点.(请利用网格作图,画出的线请用铅笔描粗描黑)

(1)过点C画AB的垂线,并标出垂线所过格点E;
(2)过点C画AB的平行线CF,并标出平行线所过格点F;
(3)直线CE与直线CF的位置关系是 ;
(4)连接AC,BC,则三角形ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
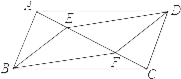
【题目】如图,E、F是ABCD对角线AC上两点,且AE=CF.
(1)求证:四边形BFDE是平行四边形.
(2)如果把条件AE=CF改为BE=DF,试问四边形BFDE还是平行四边形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个足球垂直地面向上踢,![]() (秒)后该足球的高度
(秒)后该足球的高度![]() (米)适用公式
(米)适用公式![]() .
.
(1)经多少秒时足球的高度为20米?
(2)小明同学说:“足球高度不可能达到21米!”你认为他说得对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机经销商计划同时购进一批甲、乙两种型号的手机,已知每部甲种型号的手机进价比每部乙种型号的手机进价多200元,且购进3部甲型号手机和2部乙型号手机,共需要资金9600元;
(1)求甲、乙型号手机每部进价为多少元?
(2)该店计划购进甲、乙两种型号的手机共20台进行销售,现已有顾客预定了8台甲种型号手机,且该店投入购进手机的资金不多于3.8万元,请求出有几种进货方案?并请写出进货方案.
(3)售出一部甲种型号手机,利润率为30%,乙种型号手机的售价为2520元.为了促销,公司决定每售出一台乙型号手机,返还顾客现金m元充话费,而甲型号手机售价不变,要使(2)中所有方案获利相同,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①![]() ×(﹣12);
×(﹣12);
②﹣12016﹣1÷6×[3﹣(﹣3)2]﹣|﹣2|;
(2)化简求值:2(a2b+![]() ab2)﹣(4a2b+2ab2)﹣3(ab2﹣a2b),其中a=1,b=﹣1.
ab2)﹣(4a2b+2ab2)﹣3(ab2﹣a2b),其中a=1,b=﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)a、b为有理数,且a+b、a﹣b在数轴上如图所示:
![]()
①判断:a 0,b 0,a b(用“>”“<”“=”填空).
②若x=|2a+b|﹣3|b|﹣|3﹣2a|+2|b﹣1|,求(2x2-![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )的值;
)的值;
(2)若c为有理数,![]() ,且ab﹣bc+ac=﹣99,求(3a﹣4b+2c)2+
,且ab﹣bc+ac=﹣99,求(3a﹣4b+2c)2+![]() abc的值.
abc的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】育才羽毛球队需要购买10支羽毛球拍和![]() 盒羽毛球(
盒羽毛球(![]() ),羽毛球拍市场价为150元/支,羽毛球为30元/盒,滔博运动店的优惠方案为:所有商品九折,劲浪运动店的优惠方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售.
),羽毛球拍市场价为150元/支,羽毛球为30元/盒,滔博运动店的优惠方案为:所有商品九折,劲浪运动店的优惠方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售.
(1)分别用![]() 的代数式表示在滔博运动店和劲浪运动店购买所有物品的费用;
的代数式表示在滔博运动店和劲浪运动店购买所有物品的费用;
(2)请计算说明买多少羽毛球时,到两运动店购买一样省钱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com