
����Ŀ��ij�ֻ������̼ƻ�ͬʱ����һ���ס��������ͺŵ��ֻ�����֪ÿ�������ͺŵ��ֻ����۱�ÿ�������ͺŵ��ֻ����۶�200Ԫ���ҹ���3�����ͺ��ֻ���2�����ͺ��ֻ�������Ҫ�ʽ�9600Ԫ��
(1)��ס����ͺ��ֻ�ÿ������Ϊ����Ԫ��
(2)�õ�ƻ������ס��������ͺŵ��ֻ���20̨�������ۣ������й˿�Ԥ����8̨�����ͺ��ֻ����Ҹõ�Ͷ�빺���ֻ����ʽ���3.8��Ԫ��������м��ֽ�������������д������������
(3)�۳�һ�������ͺ��ֻ���������Ϊ30%�������ͺ��ֻ����ۼ�Ϊ2520Ԫ��Ϊ�˴�������˾����ÿ�۳�һ̨���ͺ��ֻ��������˿��ֽ�mԪ�仰�ѣ������ͺ��ֻ��ۼ۲��䣬Ҫʹ(2)�����з���������ͬ����m��ֵ��
���𰸡�(1)ÿ�������ͺŵ��ֻ�����2000Ԫ��ÿ�������ͺŵ��ֻ�����1800Ԫ��(2)����һ����������8̨������12̨������������������9̨������11̨������������������10̨������10̨��(3)m=120Ԫ��
��������
(1)������ͺ��ֻ�ÿ������ΪxԪ�������ͺ��ֻ�ÿ������ΪyԪ���������⽨�����������Ϳ�������𰸣�
(2)�蹺�������ͺ��ֻ�a�����������ͺ��ֻ�(20-a)�����������ò�����1.8��Ԫ�Ҳ�����1.74��Ԫ���ʽ��������ֻ���20̨����������ʽ�飬������Ϳ��Եó����ۣ�
(3)�ֱ���������ֻ�������Ȼ�������ʹ(2)�����з���������ͬ�����m��ֵ���ɣ�
(1)������ͺ��ֻ�ÿ������ΪxԪ�������ͺ��ֻ�ÿ������ΪyԪ��
������ã�![]() ��
��
��ã�![]() ��
��
��ÿ�������ͺŵ��ֻ�����2000Ԫ��ÿ�������ͺŵ��ֻ�����1800Ԫ��
(2)�õ�ƻ����������ͺŵ��ֻ���a����������ã�
2000a+1800(20-a)��38000��
��ã�a��10��
�֡�a��8������
��a=8��9��10��
���һ����������8̨������12̨��
����������������9̨������11̨��
����������������10̨������10̨��
(3)ÿ�������ͺŵ��ֻ�������2000��30%=600Ԫ��
ÿ�������ͺŵ��ֻ�������2520-1800=720Ԫ��
��Ҫʹ(2)�����з���������ͬ
��m=720-600=120Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ��֯ȫУ1000��ѧ��������У��ȫ֪ʶ����.Ϊ�˽Ȿ��֪ʶ�����ijɼ��ֲ����,���������ȡ�˲���ѧ���ijɼ�(�÷�ȡ������,����Ϊ100��),����������ͼ��Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ(������).
���� | Ƶ�� | Ƶ�� |
50.5��60.5 | 10 | a |
60.5��70.5 | b | |
70.5��80.5 | 0.2 | |
80.5��90.5 | 52 | 0.26 |
90.5��100.5 | 0.37 | |
�ϼ� | c | 1 |

����������ṩ����Ϣ,�����������:
(1)ֱ��д��Ƶ���ֲ�����a,b,c��ֵ,��ȫƵ���ֲ�ֱ��ͼ.
(2)����ѧ���ɼ�����λ��������һ�鷶Χ��?
(3)ѧУ���Գɼ���90.5��100.5��֮���ѧ�����н���,�����ȫУ1000��ѧ����Լ�ж�������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ��ϰ��һ����1000Ԫ����һ���ľߣ��ܿ�������ϣ��ڶ��ι���ʱ����ÿ���ľߵĽ��۱ȵ�һ��������2.5Ԫ���ϰ���2500Ԫ�����˵ڶ����ľߣ��������ľߵ������ǵ�һ�ι���������2����ͬ���ܿ�������ϣ���֪�����ľߵ��ۼ۾�Ϊÿ��15Ԫ.
��1���ڶ��ι����˶��ټ��ľߣ�
��2���ľߵ��ϰ��������������й�ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=��DOC=90����OEƽ�֡�AOD�������ӳ�����OE��F.
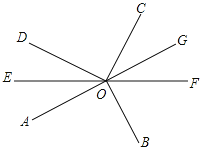
��1����AOD�͡�BOC�Ƿ���˵�����ɣ�
��2������OF�ǡ�BOC��ƽ������˵�����ɣ�
��3�������ӳ�����OA����G������OG����COF�ֳ���4��3�������ǣ����AOD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ӡˢһ��֤�飬��������ӡˢ���ɹ�ѡ���׳��շѷ�ʽ�����ư��1000Ԫ��ÿ��ӡˢ��0.5Ԫ���ҳ��շѷ�ʽ�������ư�ѣ�ÿ����ӡˢ��1.5Ԫ������Уӡ��֤��x��.
��1����ӡ��֤��3000��ʱ���׳����շ�Ϊ Ԫ���ҳ����շ�Ϊ Ԫ��
��2������ӡˢ���ٱ�֤��ʱ�����������շ���ͬ��
��3������Ϊѡ����һ��ӡˢ�����Żݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x+3���������ύ��A��B���㣬������y=��x2+bx+c��A��B���㣬�ҽ�x����������ڵ�C��
��1��ֱ��д��A��B��������ꣻ
��2���������ߵĽ���ʽ�Ͷ���D�����ꣻ
��3�������������Ƿ���ڵ�P��ʹ����PAB����ABΪֱ�DZߵ�ֱ�������Σ������ڣ�������з��������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��a��0���ĶԳ���Ϊֱ��x=1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��4ac��b2��
������![]() ����������x1=��1��x2=3��
����������x1=��1��x2=3��
��3a+c��0
����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3
����x��0ʱ��y��x���������
���н�����ȷ�ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��y1����![]() x+b�ֱ���x�ᡢy�ύ�ڵ�A����B����ֱ��l2��y2��x���ڵ�C��2��2����
x+b�ֱ���x�ᡢy�ύ�ڵ�A����B����ֱ��l2��y2��x���ڵ�C��2��2����
��1����y1��y2����ֱ��д��x��ȡֵ��Χ��
��2����P��ֱ��l1��y1����![]() x+b�ϣ��ҡ�OPC�����Ϊ3�����P�����ꣿ
x+b�ϣ��ҡ�OPC�����Ϊ3�����P�����ꣿ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB=12,P���߶�AB�����ȵ㣬Q��ֱ��AB��һ�����㣬��AQ=PQ+BQ,���߶�AQ�ij�Ϊ__________________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com