
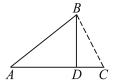
【题目】如图所示,A,B,C,D是四个小城镇,除BC外,它们之间都有笔直的公路连接,公共汽车行驶于城镇之间,其票价与路程成正比.已知各城镇间的公共汽车票价如下: A——B:10元;A——C:12.5元;A——D:8元; B——D:6元;C——D:4.5元.为了方便B,C之间的交通,在B,C之间建成一条笔直的公路,请按上述标准计算出B,C之间公共汽车的票价为多少元?
科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.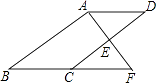
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
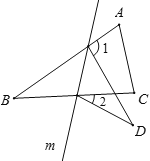
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
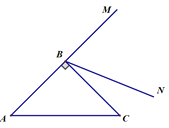
【题目】如图,BN是等腰Rt△ABC的外角∠CBM内部的一条射线,∠ABC=90°,AB=CB,点C关于BN的对称点为D,连接AD,BD,CD,其中CD,AD分别交射线BN于点E,P.
(1)依题意补全图形;
(2)若∠CBN=![]() ,求∠BDA的大小(用含
,求∠BDA的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段PB,PA与PE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形ABD中,∠A=90°,AB=AD=2,作△ABD关于直线BD对称的△CBD,已知点F为线段AB上一点,且AF=m,连接CF,作∠FCE=90°,CE交AD的延长线于点E.
(1)求证:△BCF≌△DCE;
(2)若AE=n,且mn=3,求m2+n2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( ) 
A.∠1=∠2
B.BE=DF
C.∠EDF=60°
D.AB=AF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图:在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形.按要求画出下列图形:
(1)将△ABC向右平移5个单位得到△A′B′C′;
(2)将△A′B′C′绕点A′顺时针旋转90°得到△A′DE;
(3)连结EC′,则△A′EC′是 三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com