
����Ŀ����֪��ABCΪ�ȱ������Σ���DΪֱ��BC�ϵ�һ��������D����B��C�غ�������ADΪ��������ADEF��A��D��E��F����ʱ����������ʹ��DAF=60�㣬����CF��

��1����ͼ1������D�ڱ�BC��ʱ����֤����BD=CF����AC=CF+CD��
��2����ͼ2������D�ڱ�BC���ӳ�������������������ʱ������AC=CF+CD�Ƿ������������������д��AC��CF��CD֮����ڵ�������ϵ����˵�����ɣ�
��3����ͼ3������D�ڱ�CB���ӳ�������������������ʱ����ȫͼ�Σ���ֱ��д��AC��CF��CD֮����ڵ�������ϵ��
���𰸡���1��֤������������2��AC=CF+CD��������AC��CF��CD֮����ڵ�������ϵ��AC=CF��CD����3����ͼ��������AC=CD��CF��
��������
�����������1��������֪�ó�AF=AD��AB=BC=AC����BAC=��DAF=60���������BAD=CAF��֤��BAD�ա�CAF���Ƴ�CF=BD���ɣ�
��2�������BAD=��CAF������SAS֤��BAD�ա�CAF���Ƴ�BD=CF���ɣ�
��3������ͼ�κ���SAS֤��BAD�ա�CAF���Ƴ�CF=BD������
�����������1��֤����������AFED��
��AF=AD��
�ߡ�ABC�ǵȱ������Σ�
��AB=AC=BC����BAC=60��=��DAF��
���BAC����DAC=��DAF����DAC��
����BAD=��CAF��
������BAD����CAF��
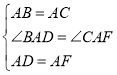
���BAD�ա�CAF��
��CF=BD��
��CF+CD=BD+CD=BC=AC��
����BD=CF����AC=CF+CD��
��2���⣺AC=CF+CD��������AC��CF��CD֮����ڵ�������ϵ��AC=CF��CD��
�����ǣ�����1��֪��AB=AC=BC��AD=AF����BAC=��DAF=60�㣬
���BAC+��DAC=��DAF+��DAC��
����BAD=��CAF��
������BAD����CAF��
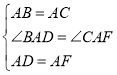 ��
��
���BAD�ա�CAF��
��BD=CF��
��CF��CD=BD��CD=BC=AC��
��AC=CF��CD��
��3��AC=CD��CF�������ǣ�
�ߡ�BAC=��DAF=60�㣬
���DAB=��CAF��
������BAD����CAF��
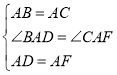 ��
��
���BAD�ա�CAF��
��CF=BD��
��CD��CF=CD��BD=BC=AC��
��AC=CD��CF��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ת����ת�̣�ÿ��ת�̷ֳ�������ͬ�����Σ�Ϳɫ�����ͼ��ʾ��ָ���λ�ù̶���ͬʱת������ת�̣��ش��������⣺

Բ1 Բ2
Բ2 Բ1 | |||
(1)��ȫ����Բ1�����п��ܽ���� �֣��ֱ��� ��
Բ2�����п��ܽ���� �֣��ֱ��� .
(2)д����ת��ֹͣ��ָ��ָ��ͬ����ɫ����ĸ��ʺ�������һָ��ָ���ɫ����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
�л����㴫ͳ�Ļ����л�����ġ������͡��ꡱ��Ϊ�������㴫ͳ�Ļ���ijУ���������μǡ��͡��������塷�����ף�����ÿ�ס����μǡ��ļ۸��ÿ�ס��������塷�ļ۸��40Ԫ����3200Ԫ�����������塷����������2400Ԫ�������μǡ�������2������ÿ�ס��������塷�ļ۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����װ�������ֱ�д������1��2��3��С�����ǵ���״����С���ʵص���ȫ��ͬ���ȴӺ��������ȡ��һ��С�������ֺ�Żغ��ӣ�ҡ�Ⱥ������ȡ��һ��С�������֣������û�����ͼ���б��ķ������������¼��ĸ��ʣ�
��1������ȡ��С���ϵ�������ͬ�ĸ��ʣ�
��2������ȡ��С���ϵ�����֮�ʹ���3�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������ABC�ĵ�Ϊ30������BCΪֱ���ġ�O��ױ�AB���ڵ�D����D��DE��AC������ΪE��
��1��֤����DEΪ��O�����ߣ�
��2������OE����BC=4������OEC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪ������ABCD�����ģ�BEƽ�֡�DBC��DC�ڵ�E���ӳ�BC����F��ʹFC=EC������DF��BE���ӳ����ڵ�H������OH��DC�ڵ�G������HC���������ĸ������У���OH��BF����GH=![]() BC����BF=2OD���ܡ�CHF=45������ȷ���۵ĸ���Ϊ( )
BC����BF=2OD���ܡ�CHF=45������ȷ���۵ĸ���Ϊ( )

A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ÿ̨���۷ֱ�Ϊ190Ԫ��160Ԫ��A��B�����ͺŵĵ���ȣ��±��ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 2̨ | 6̨ | 1840Ԫ |
�ڶ��� | 5̨ | 7̨ | 2840 Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=��������-�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����������ٲɹ��������ͺŵĵ���ȹ�40̨����40̨�����ȫ���۳�����������2660Ԫ����A���ͺŵĵ��������Ҫ�ɹ�����̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ A(0��a)��B(b��0)��a��b ����.a+b=4��a-b= 12��
��1���� a��b ��ֵ��
��2��������������һ�� D��ʹ������ ABD ��������������� OAB �����һ�룬 �� D �����ꣻ
��3������BAO ƽ�������ABC ƽ���� BE �ķ����ӳ��߽��� P �㣬���P �Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�x2����m��3��x��m=0
��1��֤��ԭ��������������ȵ�ʵ������
��2����������y=x2����m��3��x��m��x�ύ��A��x1��0����B��x2��0�����㣬��A��B�����ľ����Ƿ����������Сֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ���������ʾ��AB=|x1��x2|��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com