
【题目】某商店从厂家以每件21元的价格购进一批商品。若每件商品的售价为![]() 元,则可卖出
元,则可卖出![]() 件,但物价局限定每件商品的售价不能超过进价的120%。若该商店计划从这批商品中获取400元利润(不计其他成本),问需要卖出多少件商品,此时的售价是多少?
件,但物价局限定每件商品的售价不能超过进价的120%。若该商店计划从这批商品中获取400元利润(不计其他成本),问需要卖出多少件商品,此时的售价是多少?
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系内一点M(x,y)(x≠0),若![]() 则称k为点M的“倾斜比”,如图,⊙B与y轴相切于点A,点B的坐标为(3,5),点P为⊙B上的动点,则点P的“倾斜比”k的最小值是( )
则称k为点M的“倾斜比”,如图,⊙B与y轴相切于点A,点B的坐标为(3,5),点P为⊙B上的动点,则点P的“倾斜比”k的最小值是( )
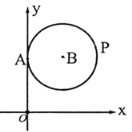
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过A、C、D三点的圆O交AB于点E,连接DE、CE,∠BCE=∠CDE.
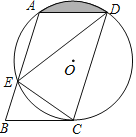
(1)求证:直线BC为圆O的切线;
(2)猜想AD与CE的数量关系,并说明理由;
(3)若BC=2,∠BCE=30°,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
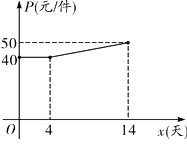
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )
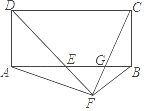
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给![]() 人.
人.
(1)求第一轮后患病的人数;(用含![]() 的代数式表示)
的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
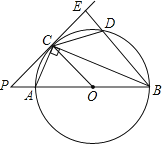
【题目】在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是![]() 上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
(1)求证:∠PCA=∠PBC;
(2)若PC=8,PA=4,∠ECD=∠PCA,以点C为圆心,半径为5作⊙C,试判断⊙C与直线BD的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com