
【题目】如图,在平行四边形ABCD中,过A、C、D三点的圆O交AB于点E,连接DE、CE,∠BCE=∠CDE.
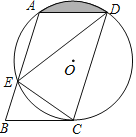
(1)求证:直线BC为圆O的切线;
(2)猜想AD与CE的数量关系,并说明理由;
(3)若BC=2,∠BCE=30°,求阴影部分面积.
【答案】(1)见解析;(2)AD=EC,理由见解析;(3)![]()
【解析】
(1)作直径CH,连接EH,根据圆周角定理可证明∠ECH+∠EHC=90°,∠EDC=∠EHC,然后证明∠BCH=90°即可;
(2)猜想:AD=CE,根据平行四边形的性质得到∠AED=∠CDE,然后证明![]() 即可;
即可;
(3)根据平行四边形的性质求出∠BCE=∠CDE=∠AED=30°,然后可得∠AOD=60°,证明△AOD是等边三角形即可解决问题;
(1)证明:作直径CH,连接EH.
∵CH是直径,
∴∠CEH=90°,
∴∠ECH+∠EHC=90°,
∵∠BCE=∠EDC,∠EDC=∠EHC,
∴∠BCE+∠ECH=90°,
∴∠BCH=90°,
∴BC⊥CH,
∴BC是⊙O的切线;
(2)解:猜想:AD=EC.
理由:∵四边形ABCD是平行四边形,
∴AE∥CD,
∴∠AED=∠CDE,
∴![]() ,
,
∴AD=EC;
(3)解:连接OA,OD,
∵四边形ABCD是平行四边形,
∴BC=AD=2,AB∥DC,
∴∠AED=∠CDE,
∴∠BCE=∠CDE=∠AED=30°,
∴∠AOD=2∠AED=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴OA=OD=AD=2,
∴S阴=S扇形OAD﹣S△AOD
=![]()
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c的对称轴l交x轴于点A.
(1)若此抛物线经过点(1,2),当点A的坐标为(2,0)时,求此抛物线的解析式;
(2)抛物线y=x2+bx+c交y轴于点B,将该抛物线平移,使其经过点A,B,且与x轴交于另一点C.若b2=2c,b≤﹣1,比较线段OB与OC+![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
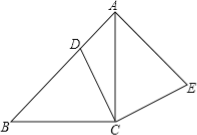
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
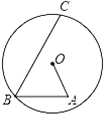
【题目】如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
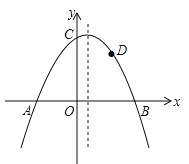
【题目】如图,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A,B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的函数关系式;
(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上是否存在一点P,使得△BDP的周长最短?若存在,求点P的坐标;若不存在,请说明理由.
(3)求出△ABC外接圆心M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以每件21元的价格购进一批商品。若每件商品的售价为![]() 元,则可卖出
元,则可卖出![]() 件,但物价局限定每件商品的售价不能超过进价的120%。若该商店计划从这批商品中获取400元利润(不计其他成本),问需要卖出多少件商品,此时的售价是多少?
件,但物价局限定每件商品的售价不能超过进价的120%。若该商店计划从这批商品中获取400元利润(不计其他成本),问需要卖出多少件商品,此时的售价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com