
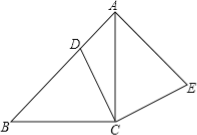
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
【答案】(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论。
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形。
【解析】
(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论。
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形。
证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°。
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE。
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE。
∵在△BCD和△ACE中, ,
,
∴△BCD≌△ACE(SAS)。∴∠B=∠CAE=45°。
∴∠BAE=45°+45°=90°。∴AB⊥AE。
(2)∵BC2=ADAB,BC=AC,∴AC2=ADAB。∴![]() 。
。
∵∠DAC=∠CAB,∴△DAC∽△CAB。∴∠CDA=∠BCA=90°。
∵∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形。
∵CD=CE,∴四边形ADCE为正方形。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①b<0;②a+b+c<0;③4a-2b+c<0;④2a-b<0,其中正确的有______.(填代号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(1)求m,k的值;
(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=![]() 的图象于点N.
的图象于点N.
①当a=4时,求MN的长;
②若PM>PN,结合图象,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的公路![]() 旁有一座山,为方便运输货物现要从公路
旁有一座山,为方便运输货物现要从公路![]() 上的
上的![]() 处开凿隧道修通一条公路到
处开凿隧道修通一条公路到![]() 处,已知点
处,已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() ,与公路上另-停靠站
,与公路上另-停靠站![]() 的距离为
的距离为![]() ,停靠站
,停靠站![]() 之间的距离为
之间的距离为![]() ,且
,且![]()
![]() 求修建的公路
求修建的公路![]() 的长;
的长;
![]() 若公路
若公路![]() 修通后,辆货车从
修通后,辆货车从![]() 处经过
处经过![]() 点到
点到![]() 处的路程是多少?
处的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b+c=0;③a﹣b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.其中结论正确的有______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 若点
若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当k取不同的值时,y关于x的函数y=kx+2(k≠0)的图象为总是经过点(0,2)的直线,我们把所有这样的直线合起来,称为经过点(0,2)的“直线束”.那么,下面经过点(﹣1,2)的直线束的函数式是( )

A. y=kx﹣2(k≠0) B. y=kx+k+2(k≠0)
C. y=kx﹣k+2(k≠0) D. y=kx+k﹣2(k≠0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com