
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?

科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E. F.

(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
(1)在下列坐标系中画出这个图案;
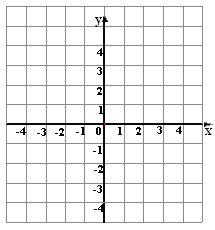
(2)若将上述各点的横坐标保持不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连接起来,所得的图案与原图案相比有什么变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
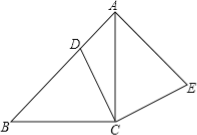
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).

(1)直接写出这两个二次函数的表达式;
(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;
(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 .

(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
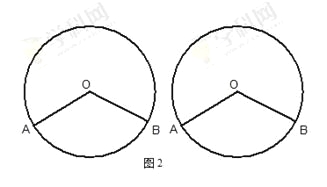
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC.其中正确结论的番号是( )
EC.其中正确结论的番号是( )

A.①②④⑤B.①②③④⑤C.①②④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
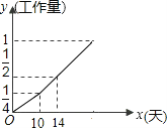
【题目】甲、乙两个工程队完成某项工程,首先是甲队单独做了10天,然后乙队加入合作,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系.
(1)求甲、乙两队合作完成剩下的全部工程时,工作量y与天数x间的函数关系式;
(2)求实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com