
【题目】 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=![]() EC.其中正确结论的番号是( )
EC.其中正确结论的番号是( )

A.①②④⑤B.①②③④⑤C.①②④D.①④
【答案】A
【解析】
过P作PG⊥AB于点G,根据正方形对角线的性质及题中的已知条件,证明△AGP≌△FPE后即可证明①AP=EF;④∠PFE=∠BAP;在此基础上,根据正方形的对角线平分对角的性质,在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,求得⑤DP=![]() EC.
EC.
证明:过P作PG⊥AB于点G,
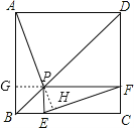
∵点P是正方形ABCD的对角线BD上一点,
∴GP=EP,
在△GPB中,∠GBP=45°,
∴∠GPB=45°,
∴GB=GP,
同理,得
PE=BE,
∵AB=BC=GF,
∴AG=AB-GB,FP=GF-GP=AB-GB,
∴AG=PF,
∴△AGP≌△FPE,
①∴AP=EF;
∠PFE=∠GAP
∴④∠PFE=∠BAP,
②延长AP到EF上于一点H,
∴∠PAG=∠PFH,
∵∠APG=∠FPH,
∴∠PHF=∠PGA=90°,即AP⊥EF;
③∵点P是正方形ABCD的对角线BD上任意一点,∠ADP=45度,
∴当∠PAD=45度或67.5度或90度时,△APD是等腰三角形,
除此之外,△APD不是等腰三角形,故③错误.
∵GF∥BC,
∴∠DPF=∠DBC,
又∵∠DPF=∠DBC=45°,
∴∠PDF=∠DPF=45°,
∴PF=EC,
∴在Rt△DPF中,DP2=DF2+PF2=EC2+EC2=2EC2,
∴⑤DP=![]() EC.
EC.
∴其中正确结论的序号是①②④⑤.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(1)求m,k的值;
(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=![]() 的图象于点N.
的图象于点N.
①当a=4时,求MN的长;
②若PM>PN,结合图象,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 若点
若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个金属棒在不同温度下,其长度也不同,其变化情况如下表:
温度/℃ | … | -5 | 0 | 5 | 10 | 15 | … |
长度/ | … | 13.9 | 13.95 | 14 | 14.05 | 14.1 | … |
(1)上述两个变量中,自变量是 ;
(2)设自变量为![]() ,因变量为
,因变量为![]() ,求出
,求出![]() 关于
关于![]() 的解析式;
的解析式;
(3)当温度为30℃时,求金属棒的长度;
(4)若某天金属棒的长度是14.18![]() ,则当天的气温约是多少℃?
,则当天的气温约是多少℃?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD.
(1)求证:△PDO≌△GEO;
(2)求DP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合)。若四边形OBCD是平行四边形时,那么![]() 的数量关系是________________.
的数量关系是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当k取不同的值时,y关于x的函数y=kx+2(k≠0)的图象为总是经过点(0,2)的直线,我们把所有这样的直线合起来,称为经过点(0,2)的“直线束”.那么,下面经过点(﹣1,2)的直线束的函数式是( )

A. y=kx﹣2(k≠0) B. y=kx+k+2(k≠0)
C. y=kx﹣k+2(k≠0) D. y=kx+k﹣2(k≠0)
查看答案和解析>>
科目:初中数学 来源: 题型:
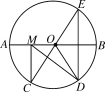
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com