练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】 如图，矩形ABCD中，AB=10，BC=8，P为AD上一点，将△ABP沿BP翻折至△EBP（点A落在点E处），PE与CD相交于点O，且OE=OD．

    （1）求证：△PDO≌△GEO；

    （2）求DP的长．

    【答案】（1）详见解析；（2）DP=

    【解析】

    （1）由“ASA”可证△PDO≌△GEO；

    （2）由勾股定理可求AP的长，即可求DP的长．

    证明：在△ODP和△OEG中，

    ∴△PDO≌△GEO（ASA）

    （2）∵△PDO≌△GEO；

    ∴OP=OG，PD=GE，

    ∴DG=EP，

    设AP=EP=x，则PD=GE=8-x，DG=x，

    ∴CG=10-x，BG=10-（8-x）=2+x，

    根据勾股定理得：BC2+CG2=BG2，

    即64+（10-x）2=（2+x）2，

    解得x=

    ∴DP=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

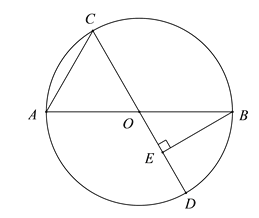
    【题目】如图，点C是以AB为直径的⊙O上一动点，过点C作⊙O直径CD，过点B作BE⊥CD于点E．已知AB=6cm，设弦AC的长为xcm，B，E两点间的距离为ycm（当点C与点A或点B重合时，y的值为0）．

    小冬根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．

    下面是小冬的探究过程，请补充完整：

    （1）通过取点、画图、测量，得到了x与y的几组值，如下表：

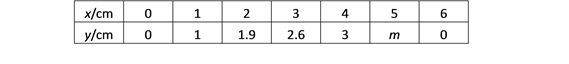
    经测量m的值是（保留一位小数）．

    （2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；

    （3）在（2）的条件下，当函数图象与直线相交时（原点除外），∠BAC的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAP+∠APD=180°，∠1=∠2，求证：∠E=∠F．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线C：y=x2+（2m﹣1）x﹣2m．

    （1）若m=1，抛物线C交x轴于A，B两点，求AB的长；

    （2）若一次函数y=kx+mk的图象与抛物线C有唯一公共点，求m的取值范围；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；④∠PFE=∠BAP；⑤PD=EC．其中正确结论的番号是（　　）

    A.①②④⑤B.①②③④⑤C.①②④D.①④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA=3，OB=2OA，C为直线y=2x与直线AB的交点，点D在线段OC上，OD=．

    （1）求点C的坐标；

    （2）若P为线段AD上一动点（不与A、D重合）．P的横坐标为x，△POD的面积为S，请求出S与x的函数关系式；

    （3）若F为直线AB上一动点，E为x轴上一点，是否存在以O、D、E、F为顶点的四边形是平行四边形？若存在，写出点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，从热气球C处测得地面A，B两点的俯角分别为30°，45°，此时热气球C处所在位置到地面上点A的距离为400米．求地面上A，B两点间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某市为方便行人过马路，打算修建一座高为4x（m）的过街天桥．已知天桥的斜面坡度i=1：0.75是指坡面的铅直高度DE（CF）与水平宽度AE（BF）的比，其中DC∥AB，CD=8x（m）．

    （1）请求出天桥总长和马路宽度AB的比；

    （2）若某人从A地出发，横过马路直行（A→E→F→B）到达B地，平均速度是2.5m/s；返回时从天桥由BC→CD→DA到达A地，平均速度是1.5m/s，结果比去时多用了12.8s，请求出马路宽度AB的长．

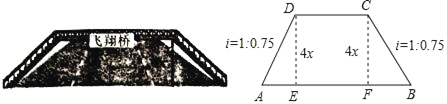
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为落实“垃圾分类”，环卫部门要求垃圾要按A,B,C三类分别装袋,投放，其中A类指废电池,过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类.

    (1)直接写出甲投放的垃圾恰好是A类的概率；

    (2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.

    查看答案和解析>>

    同步练习册答案