
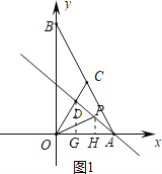
【题目】 如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=3,OB=2OA,C为直线y=2x与直线AB的交点,点D在线段OC上,OD=![]() .
.
(1)求点C的坐标;
(2)若P为线段AD上一动点(不与A、D重合).P的横坐标为x,△POD的面积为S,请求出S与x的函数关系式;
(3)若F为直线AB上一动点,E为x轴上一点,是否存在以O、D、E、F为顶点的四边形是平行四边形?若存在,写出点F的坐标;若不存在,请说明理由.

【答案】(1)点C坐标为(![]() ,3);(2)S =
,3);(2)S =![]() x-
x-![]() ;(3)存在,点F的坐标为(2,2)或(4,-2).
;(3)存在,点F的坐标为(2,2)或(4,-2).
【解析】
(1)根据题意求出A、B的坐标再求直线AB解析式,把直线AB与直线OC的方程联立方程组,求得的解即为点C坐标.
(2)由OD=![]() 及点D在直线y=2x上求得点D坐标,进而求得直线AD解析式,得到点P纵坐标的表示,用x表示△AOP的面积.利用S等于△AOD与△AOP面积差即求得S与x的函数关系式.
及点D在直线y=2x上求得点D坐标,进而求得直线AD解析式,得到点P纵坐标的表示,用x表示△AOP的面积.利用S等于△AOD与△AOP面积差即求得S与x的函数关系式.
(3)由于OD是固定的,所以以OD为平行四边形的边或对角线作为分类讨论的依据.画图即得到点F的纵坐标与点D纵坐标相等或互为相反数,把纵坐标代入直线AB解析式即求得F的横坐标.
解:(1)∵OA=3,点A和点B分别在x轴和y轴的正半轴上
∴A(3,0),OB=3OA=6
∴B(0,6)
设直线AB解析式为:y=kx+b
∴![]() 解得:
解得:![]()
∴直线AB解析式为:y=-2x+6
∵![]() 解得:
解得:![]()
∴点C坐标为(![]() ,3)
,3)
(2)过点D作DG⊥x轴于点G,过点P作PH⊥x轴于点H
∵点D在线段OC上,直线OC解析式为y=2x
∴设点D(d,2d)(0<d<![]() )
)
∴OD=![]()
∴d=1
∴D(1,2),DG=2
设直线AD解析式为:y=ax+c
∴![]() 解得:
解得:![]()
∴直线AD解析式为:y=-x+3
∵点P在线段AD上,且横坐标为x
∴OH=x,PH=yP=-x+3
∴S=S△AOD-S△AOP=![]() OADG-
OADG-![]() OAPH=
OAPH=![]() OA(DG-PH)=
OA(DG-PH)=![]() ×3×(2+x-3)=
×3×(2+x-3)=![]() x-
x-![]()
(3)存在以O、D、E、F为顶点的四边形是平行四边形.
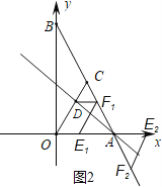
①当OD为平行四边形的边时,如图2,
∴|yF|=yD=2
∵|-2x+6|=2解得:x1=2,x2=4
∴F(2,2)或(4,-2)
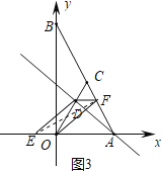
②当OD为平行四边形的对角线时,如图3,
∴DF∥x轴,yF=yD=2
∴F(2,2)
综上所述,点F的坐标为(2,2)或(4,-2).


科目:初中数学 来源: 题型:
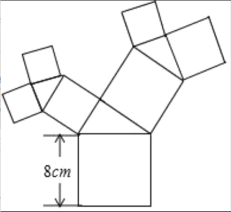
【题目】如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为![]() ,则图中所有正方形的面积的和是___________
,则图中所有正方形的面积的和是___________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
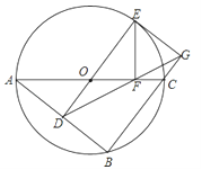
【题目】如图,⊙O是△ABC的外接圆,AC是直径,过O作OD∥BC交AB于点D.延长DO交⊙O于点E,作EF⊥AC于点F.连接DF并延长交直线BC于点G,连接EG.
(1)求证:FC=GC;
(2)求证:四边形EDBG是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从运河码头出发,沿该公路开往薰衣草庄园,途中停靠生态文化园(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从运河码头发车.小聪周末到该风景区游玩,上午7:40到达运河码头,因还没到班车发车时间,于是从景区运河码头出发,沿该公路步行25分钟后到达生态文化园.离运河码头的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
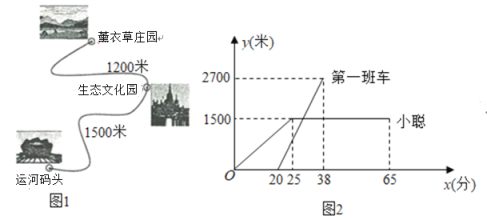
(1)求第一班车离运河码头的路程![]() (米)与时间
(米)与时间![]() (分)的函数表达式.
(分)的函数表达式.
(2)求第一班车从运河码头到达生态文化园所需的时间.
(3)小聪在生态文化园游玩40分钟后,想坐班车到薰衣草庄园,则小聪最早能够坐上第几班车?如果他坐这班车到薰衣草庄园,比他在生态文化园游玩结束后立即步行到薰衣草庄园提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,矩形ABCD中,AB=10,BC=8,P为AD上一点,将△ABP沿BP翻折至△EBP(点A落在点E处),PE与CD相交于点O,且OE=OD.
(1)求证:△PDO≌△GEO;
(2)求DP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
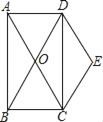
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从下列算式:①![]() ;②26÷23=4;③ -12018=1;④ (-
;②26÷23=4;③ -12018=1;④ (-![]() )2=3;⑤a+a=a2中随机抽取一个,运算结果正确的概率是( )
)2=3;⑤a+a=a2中随机抽取一个,运算结果正确的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com