
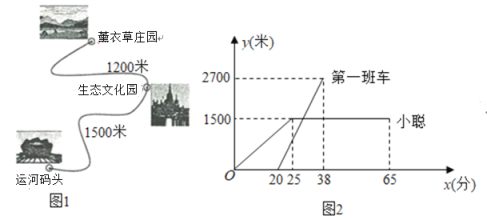
����Ŀ��ij�羰���ڵĹ�·��ͼ1��ʾ������������ѵİ�����˺���ͷ�������ظù�·�����²�ׯ��;��ͣ����̬�Ļ������³�ʱ����Բ��ƣ�����һ�����8�㷢�����Ժ�ÿ��10������һ����˺���ͷ������С����ĩ���÷羰�����棬����7:40�����˺���ͷ����û�������ʱ�䣬���ǴӾ����˺���ͷ�������ظù�·����25���Ӻ���̬�Ļ������˺���ͷ��·��![]() ���ף���ʱ��
���ף���ʱ��![]() ����)�ĺ�����ϵ��ͼ2��ʾ��
����)�ĺ�����ϵ��ͼ2��ʾ��
��1�����һ����˺���ͷ��·��![]() ���ף���ʱ��
���ף���ʱ��![]() ���֣��ĺ�������ʽ��
���֣��ĺ�������ʽ��
��2�����һ����˺���ͷ������̬�Ļ������ʱ�䣮
��3��С������̬�Ļ�����40���Ӻ���������²�ׯ����С�������ܹ����ϵڼ��?������������²�ׯ����������̬�Ļ�����������������е��²�ׯ�����˼�����?������ÿһ��ٶȾ���ͬ��С�ϲ����ٶȲ��䣩
���𰸡���1��![]() ����2����һ����˺���ͷ������̬�Ļ�����ʱ��10���ӣ���3����������̬�Ļ�����������������е��²�ׯ������7���ӣ�
����2����һ����˺���ͷ������̬�Ļ�����ʱ��10���ӣ���3����������̬�Ļ�����������������е��²�ׯ������7���ӣ�
��������
��1����y=kx+b�����ô���ϵ������⼴�ɣ�
��2����y=1500���루1���Ľ���ʽ���x���ɣ�
��3����С�������˵�n���30-25+10��n-1����40�����n��4.5���ɵ�С�������˵�5����ٸ��ݡ�·�̡��ٶ���ʱ��Ĺ�ϵ����ɣ�
�⣺��1��������ã����躯������ʽΪ��![]() ��
��
��![]() ��
��![]() ����
����![]() ����
����![]() �����
�����![]() ��
��
���һ����˺���ͷ��·��![]() ���ף���ʱ��
���ף���ʱ��![]() ���֣��ĺ�������Ϊ
���֣��ĺ�������Ϊ![]() ��
��
��2����![]() ����
����![]() �����
�����![]() ��
��
![]() ���֣���
���֣���
���һ����˺���ͷ������̬�Ļ�����ʱ��10���ӣ�
��3����С�������˵�![]() �����
�����
![]() �����
�����![]() ��
��
��С�������˵�5���
�ȳ���ʱ��Ϊ5���ӣ��������ʱ��Ϊ��![]() ���֣���
���֣���
��������ʱ�䣺![]() ���֣���
���֣���
![]() ���֣���
���֣���
���������̬�Ļ�����������������е��²�ׯ������7���ӣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�б��
���![]() �����
�����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �����ƽ�����ڵ�
�����ƽ�����ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��ֱ
��ֱ![]() ���ӳ������
���ӳ������![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() �����в��н��ۣ���
�����в��н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�ĸ����ǣ� ��
��������ȷ�ĸ����ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������һ���߳�Ϊn��n��2�����������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬 ��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ����أ�
����̽����Ҫ�о���������⣬���Dz����ȴ��������֣������ҵ�һ�����
̽��һ����һ���߳�Ϊ2���������ε�������ƽ�֣����Ӹ����е㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
��ͼ1�����ӱ߳�Ϊ2���������������ߵ��е㣬�������£�����1+2+3=6����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2��������1+2=3�����߶���Ϊ3��3=9�����߳�Ϊ2������������1�����߶���Ϊ3�����ܹ���3����1+2+1��=2����1+2+3��=12���߶Σ�

̽��������һ���߳�Ϊ3���������ε����������ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
��ͼ2�����ӱ߳�Ϊ3���������������ߵĶ�Ӧ���ȷֵ㣬�������£�����1+2+3+4=10����㣮�߳�Ϊ1���������Σ���һ����1�����ڶ�����2������������3��������1+2+3=6�����߶���Ϊ3��6=18�����߳�Ϊ2������������1+2=3�����߶���Ϊ3��3=9�����߳�Ϊ3������������1�����߶���Ϊ3�����ܹ���3����1+2+3+1+2+1��=3����1+2+3+4��=30���߶Σ�
̽������
�����������ķ�����̽�����߳�Ϊ4���������ε��������ĵȷ֣�ͼ3�������Ӹ��߶�Ӧ�ĵȷֵ㣬�������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
������ʾ��ͼ����д��̽�����̣�
��������
�����������ķ�����̽����һ���߳�Ϊn��n��2�����������ε�������n�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣���д��̽�����̣�
ʵ��Ӧ�ã�
��һ���߳�Ϊ30���������ε���������ʮ�ȷ֣����Ӹ��߶�Ӧ�ĵȷֵ㣬��������α��ʷֵ������еĽ��������߶����ֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���̶ӳа���ij���ȫ��1755�Ĺ�������ʩ�����ס�����������ֱ�Ӷ���������ͬʱ�������֪���������ƽ��ÿ�����0��6�ף�����5��ʩ�������鹲�����45�ף�
��1����ס�����������ƽ��ÿ������������?
��2��Ϊ�ӿ칤�̽��ȣ�ͨ���Ľ�ʩ����������ʣ��Ĺ����У�����ƽ��ÿ���ܱ�ԭ������0��2�ף�����ƽ��ÿ���ܱ�ԭ������0��3�ף�����츹����ȣ��ܹ���ԭ�����ö������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
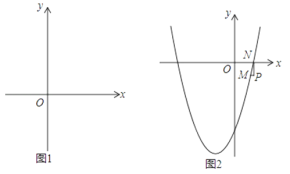
����Ŀ����֪������C��y=x2+��2m��1��x��2m��
��1����m=1��������C��x����A��B���㣬��AB�ij���
��2����һ�κ���y=kx+mk��ͼ����������C��Ψһ�����㣬��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�г���Ʒѷ�����ͼ��ʾ��x��km����ʾ��ʻ��̣�y��Ԫ����ʾ���ѣ������ͼ��ش���������⣺

��1����������Ƕ���Ԫ����x��3ʱ����y����x�ĺ�����ϵʽ��
��2����ij�˿���һ�γ˳���ij���Ϊ32Ԫ������λ�˿ͳ˳�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ����ƽ��ֱ������ϵ�У���A�͵�B�ֱ���x���y����������ϣ�OA=3��OB=2OA��CΪֱ��y=2x��ֱ��AB�Ľ��㣬��D���߶�OC�ϣ�OD=![]() ��
��
��1�����C�����ꣻ
��2����PΪ�߶�AD��һ���㣨����A��D�غϣ���P�ĺ�����Ϊx����POD�����ΪS�������S��x�ĺ�����ϵʽ��
��3����FΪֱ��AB��һ���㣬EΪx����һ�㣬�Ƿ������O��D��E��FΪ������ı�����ƽ���ı��Σ������ڣ�д����F�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���2x2+2x��1=0��������Ϊx1��x2����x1��x2�����н�����ȷ���ǣ�������
A. x1+x2=1 B. x1x2=��1 C. |x1|��|x2| D. x12+x1=![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ϊ�Ӽס��������˶�Ա��ѡ��һ�˲μӱ����������ǽ��������β��ԣ����Գɼ����±�����λ��������
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ƽ���ɼ� | ��λ�� | |
�� | 10 | 8 | 9 | 8 | 10 | 9 | 9 | �� |
�� | 10 | 7 | 10 | 10 | 9 | 8 | �� | 9.5 |
��1����ɱ�����բ� ���� ��
��2�����������β��Գɼ��ķ��
��3���������β��Գɼ�����Ϊ![]() ������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�
������Ϊ�Ƽ�˭�μӱ��������ʣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com