
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.

【答案】(1)a=-1,b=1;(2)d=﹣t2+![]() t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣
t+5(0<t<3);(3)点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).
【解析】试题分析:
(1)把A、B两点的坐标代入抛物线的解析式列出关于a、b的二元一次方程组,解方程组即可求得a、b的值;
(2)如下图2、过点P作PG⊥DE于点K,交x轴于点G,作DK⊥PG于点K,则由已知条件易得∠BCO=∠PDK,由此可得tan∠PDK=![]() =tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=
=tan∠BCO,结合OB=3,OC=6,DK=t+2可得PK=![]() DK=
DK=![]() (t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(t+2);再证四边形ADKG是矩形可得KG=AD=d=PG-PK结合PG=-t2+t+6即可得到d与t间的函数关系式了,由点P在第一象限的图象上可得0<t<3;
(3)如下图3,过点P作PH⊥AD于点H交y轴于点R,由已知条件易证△PHD≌△CNE,从而可得PH=CN,结合CN=OC-ON,PH=t+2可得关于t的方程t+2=t2﹣![]() t+1,解方程可得t1=2,t2=﹣
t+1,解方程可得t1=2,t2=﹣![]() (舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
(舍),把t=2代入抛物线y=﹣x2+x+6=4,可得点P(2,4),由此可得PR=CR,PH=AH,从而可得∠APC=90°结合∠QPC=∠APD可得∠QPD=90°,然后分点P在第一象限的抛物线上和第三象限的抛物线上两种情况讨论计算即可得到对应的点Q的坐标.
试题解析:
(1)∵抛物线y=ax2+bx+6过点A(﹣2,0),B(3,0),则
![]() ,解得:
,解得: ![]() ,
,
故抛物线解析式为y=﹣x2+x+6;
(2)如下图2,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,
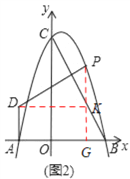
∵PD⊥BC,DE⊥y轴,∠BCO=∠PDK,OB=3,OC=6
∴tan∠BCO=tan∠PDK=![]() ,DK=t+2,PK=
,DK=t+2,PK=![]() DK=
DK=![]() (t+2),
(t+2),
∵DK∥AB,AD⊥AB,
∴四边形ADKG为矩形,
∴AD=KG,
d=AD=KG=PG﹣PK=﹣t2+t+6﹣![]() (t+2)=﹣t2+
(t+2)=﹣t2+![]() t+5(0<t<3);
t+5(0<t<3);
(3)如图3,过点P作PH⊥AD于点H,
在△PHD与△CNE中, 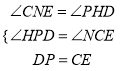 ,
,
∴△PHD≌△CNE,
∴PH=CN=OC﹣ON,
∵四边形ADON为矩形,
∴CN=6﹣(﹣t2+![]() t+5)=t2﹣
t+5)=t2﹣![]() t+1,PH=t+2,
t+1,PH=t+2,
∴t+2=t2﹣![]() t+1,
t+1,
解得t1=2,t2=﹣![]() (舍),
(舍),
把t=2代入抛物线y=﹣x2+x+6=4,
∴点P(2,4),
∵PH与y轴交于点R,PR=CR=2,
∴∠CPR=45°,PH=AH=4,
∴∠APH=45°,
∴∠APC=90°,
∵∠QPC=∠APD,
∴∠QPD=90°,
当点Q在第一象限时,过点Q作QL⊥PH于点L,
∴∠LQP=∠HPD,
∴tan∠LQP=tan∠HPD=![]() ,
,
设点Q(m,﹣m2+m+6),则PL=2﹣m,QL=﹣m2+m+2,则
![]() =
=![]() ,
,
解得m1=1,m2=2(舍),
把m=1 代入﹣m2+m+6=6,
∴Q(1,6),
当点Q在第二象限时,过点Q作QM⊥PH,
∵∠CPH=∠APH=45°∠QPC=∠APD,
∴∠QPM=∠DPH tan∠QPM=tan∠DPH=![]() ,
,
设点Q(n,﹣n2+n+6)PM=2﹣n QM=﹣n2+n+2,
∴![]() =
=![]() ,
,
解得n1=﹣![]() ,n2=2(舍),
,n2=2(舍),
把n=1﹣![]() 代入﹣n2+n+6=
代入﹣n2+n+6=![]() ,
,
∴Q(﹣![]() ,
, ![]() ).
).
综上所述,点Q坐标为Q(1,6)或Q(﹣![]() ,
, ![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】问题提出:将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点, 则该三角形被剖分的网格中的结点个数和线段数分别是多少呢?
问题探究:要研究上面的问题,我们不妨先从特例入手,进而找到一般规律
探究一:将一个边长为2的正三角形的三条边平分,连接各边中点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图1,连接边长为2的正三角形三条边的中点,从上往下:共有1+2+3=6个结点.边长为1的正三角形,第一层有1个,第二层有2个,共有1+2=3个,线段数为3×3=9条;边长为2的正三角形有1个,线段数为3条,总共有3×(1+2+1)=2×(1+2+3)=12条线段.

探究二:将一个边长为3的正三角形的三条边三等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
如图2,连接边长为3的正三角形三条边的对应三等分点,从上往下:共有1+2+3+4=10个结点.边长为1的正三角形,第一层有1个,第二层有2个,第三层有3个,共有1+2+3=6个,线段数为3×6=18条;边长为2的正三角形有1+2=3个,线段数为3×3=9条,边长为3的正三角形有1个,线段数为3条,总共有3×(1+2+3+1+2+1)=3×(1+2+3+4)=30条线段.
探究三:
请你仿照上面的方法,探究将边长为4的正三角形的三条边四等分(图3),连接各边对应的等分点,该三角形被剖分的网格中的结点个数和线段数分别是多少?
(画出示意图,并写出探究过程)
问题解决:
请你仿照上面的方法,探究将一个边长为n(n≥2)的正三角形的三条边n等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?(写出探究过程)
实际应用:
将一个边长为30的正三角形的三条边三十等分,连接各边对应的等分点,则该三角形被剖分的网格中的结点个数和线段数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=3,OB=2OA,C为直线y=2x与直线AB的交点,点D在线段OC上,OD=![]() .
.
(1)求点C的坐标;
(2)若P为线段AD上一动点(不与A、D重合).P的横坐标为x,△POD的面积为S,请求出S与x的函数关系式;
(3)若F为直线AB上一动点,E为x轴上一点,是否存在以O、D、E、F为顶点的四边形是平行四边形?若存在,写出点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程2x2+2x﹣1=0的两个根为x1,x2,且x1<x2,下列结论正确的是( )
A. x1+x2=1 B. x1x2=﹣1 C. |x1|<|x2| D. x12+x1=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便行人过马路,打算修建一座高为4x(m)的过街天桥.已知天桥的斜面坡度i=1:0.75是指坡面的铅直高度DE(CF)与水平宽度AE(BF)的比,其中DC∥AB,CD=8x(m).
(1)请求出天桥总长和马路宽度AB的比;
(2)若某人从A地出发,横过马路直行(A→E→F→B)到达B地,平均速度是2.5m/s;返回时从天桥由BC→CD→DA到达A地,平均速度是1.5m/s,结果比去时多用了12.8s,请求出马路宽度AB的长.
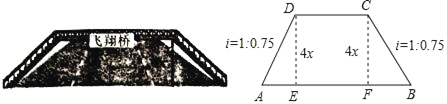
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线m∥n,点A,B分别是直线m,n上任意两点,在直线n上取一点C,使BC=AB,连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)如图1,当点E在线段AC上,且∠AFE=30°时,求∠ABE的度数;
(2)若点E是线段AC上任意一点,求证:EF=BE;
(3)如图2,当点E在线段AC的延长线上时,若∠ABC=90°,请判断线段EF与BE的数量关系,并说明理由.
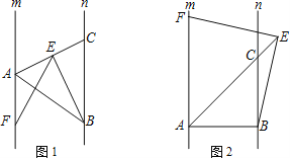
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC三边分别为![]() 、
、![]() 、
、![]() ,根据下列条件能判断△ABC为直角三角形的有 ( )
,根据下列条件能判断△ABC为直角三角形的有 ( )
①∠A=∠B+∠C;②∠A:∠B:∠C=3:4:5;③![]() ;④
;④![]() ,
,![]() ,
,![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com