
����Ŀ����ͼ��ij��Ϊ�������˹���·��������һ����Ϊ4x��m���Ĺ������ţ���֪���ŵ�б���¶�i=1��0.75��ָ�����Ǧֱ�߶�DE��CF����ˮƽ����AE��BF���ıȣ�����DC��AB��CD=8x��m����
��1������������ܳ�����·����AB�ıȣ�
��2����ij�˴�A�س����������·ֱ�У�A��E��F��B������B�أ�ƽ���ٶ���2.5m/s������ʱ��������BC��CD��DA����A�أ�ƽ���ٶ���1.5m/s�������ȥʱ������12.8s���������·����AB�ij���
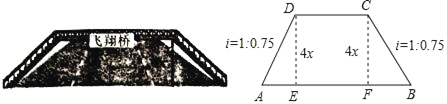
���𰸡���1��9��7����2��AB�ij�Ϊ28m.
��������
��1����֤���ı���CDEF�Ǿ��Σ���EF=DC=8x�������¶ȵĶ���ɵ�EA=BF=3x��AD=BC=5x������AB=AE+EF+BF=14x�������ܳ�����·����AB�ı�=18x��14x.(2) �ɣ�1����֪��AB=14x��AD+CD+BC=18x�������⣺![]() ,�ⷽ�̿ɵ�.
,�ⷽ�̿ɵ�.
�⣺��1����DE��AB��CF��AB��
���DEF=��CFE=90�㣬
��DE��CF��
��DC��AB��
���ı���CDEF�Ǿ��Σ�
��EF=DC=8x��
��![]() =
=![]() =
=![]() ��
��
��EA=BF=3x��
��AD=BC=5x��
��AB=AE+EF+BF=14x��
�������ܳ�����·����AB�ı�=18x��14x=9��7��
��2���ɣ�1����֪��AB=14x��AD+CD+BC=18x��
�����⣺![]() =
=![]() ��12.8��
��12.8��
���x=2��
��14x=28��
����·����AB�ij�Ϊ28m.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
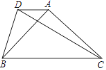
����Ŀ����ͼ������ABC�У���BAC=90�㣬AB=AC��DA��BC��tan��DBA= ![]() ����CD=2
����CD=2 ![]() �����߶�BC�ij�Ϊ________��
�����߶�BC�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
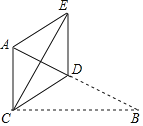
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬BC=6��CD��б��AB�ϵ����ߣ�����BCD��ֱ��CD��������ECD��λ�ã�����AE����DE��AC������AE�ij��ȵ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֹ�����ڼ䣬ij���ϻ������ij����Ѳ�ߣ�����ijһʱ����A���ӵ�ָ�Ӳ�֪ͨ�������Ƕ����������12�����B����һ�Ҳ��㴬����������ƫ��75��������ÿСʱ10������ٶȺ��У������Ա��������Ѳ�ߴ���ÿСʱ14������ٶ��ر�ƫ��ijһ�����������C���ɹ����ز��㴬����Ѳ�ߴ��ӳ������ɹ����ز��㴬���õ�ʱ���ǣ�������

A. 1Сʱ B. 2Сʱ C. 3Сʱ D. 4Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
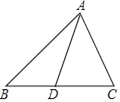
����Ŀ����ͼ������ABC�У���B=45�㣬��C=60�㣬AC=20��
��1����BC�ij��ȣ�
��2������ADC=75�㣬��CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��̫������ˮ��װ�õ�ʾ��ͼ�����ò������ȹܿ���̫����ת��Ϊ���ܣ��������ȹ���̫�����ߴ�ֱʱ������̫���ܵ�Ч����ã�����ij�û�Ҫ����ݱ�������������ʱ��̫�����������ˮƽ�ߵļнǣ�����ȷ���������ȹܵ���б�ǣ�̫�������벣�����ȹܴ�ֱ������������¼��㣺��ͼ2��AB��BC������Ϊ��B��CD��AB��FG��DE������Ϊ��G�����Ϧ�=37��50�䣬FG=30cm��CD=10cm����CF�ij������ȡ�������ο����ݣ�sin37��50���0.6l��cos37��50���079��tan37��50���0.78��
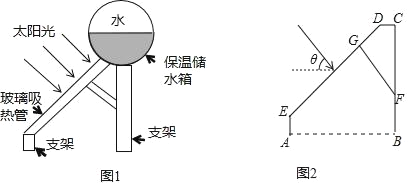
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ʳƷ��˾��һ�����з���ʳƷ�����һЩ��Ʒ��������ÿ���˰�A����ϲ������B��һ�㣩��C���Ƚ�ϲ������D���dz�ϲ�����ĸ��ȼ���ʳƷ�������ۣ�ͼ1��ͼ2�Ǹù�˾�ɼ����ݺ��Ƶ�������������ͳ��ͼ��
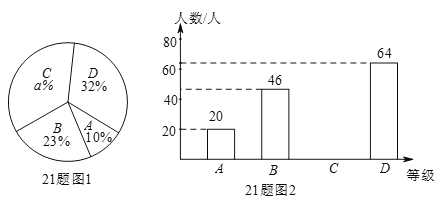
�����������ͳ��ͼ�ṩ����Ϣ���ش��������⣺
��1�����ε��������Ϊ �ˣ�
��2��ͼ1�У�a = ��C�ȼ���ռ��Բ�ĽǵĶ���Ϊ �ȣ�
��3����ֱ����ͼ�в�ȫ����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ֱ������ABCD�У�AB��BC��AD��BC����PΪDC��һ�㣬��AP��AB������C��CE��BP��ֱ��BP��E.
(1) ��![]() ����֤��
����֤��![]() ��
��
(2) ��AB��BC.
�� ��ͼ2������P��E�غ�ʱ����![]() ��ֵ��
��ֵ��
�� ��ͼ3�����DAP��ƽ����AF��ֱ��BP��F����CE��1��![]() ʱ��ֱ��д���߶�AF�ij�.
ʱ��ֱ��д���߶�AF�ij�.
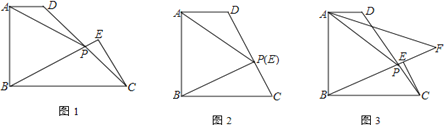
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������AOBC�����������ֱ�ΪA��0��3����O��0��0����B��3��0����C��3��3��������ԭ��Ϊλ�����ģ�����������εı߳���СΪԭ����![]() �����������ε����ĵ�����Ϊ_____��
�����������ε����ĵ�����Ϊ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com