
【题目】已知:直线m∥n,点A,B分别是直线m,n上任意两点,在直线n上取一点C,使BC=AB,连接AC,在直线AC上任取一点E,作∠BEF=∠ABC,EF交直线m于点F.
(1)如图1,当点E在线段AC上,且∠AFE=30°时,求∠ABE的度数;
(2)若点E是线段AC上任意一点,求证:EF=BE;
(3)如图2,当点E在线段AC的延长线上时,若∠ABC=90°,请判断线段EF与BE的数量关系,并说明理由.
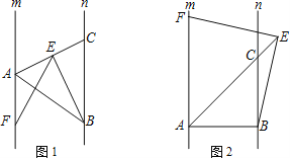
【答案】(1)30°;(2)见解析;(3)EF=BE,见解析
【解析】
(1)根据平行线的性质得到∠FAB=∠ABC,根据三角形内角和定理解答即可;
(2)以点E为圆心,以EA为半径画弧交直线m于点M,连接EM,证明△AEB≌△MEF,根据全等三角形的性质证明;
(3)在直线m上截取AN=AB,连接NE,证明△NAE≌△ABE,根据全等三角形的性质得到EN=EB,∠ANE=∠ABE,证明EN=EF,等量代换即可.
(1)∵m∥n,
∴∠FAB=∠ABC,
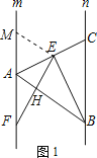
∵∠BEF=∠ABC,
∴∠FAB=∠BEF,
∵∠AHF=∠EHB,∠AFE=30°,
∴∠ABE=30°;
(2)如图1,以点E为圆心,以EA为半径画弧交直线m于点M,连接EM,
∴EM=EA,
∴∠EMA=∠EAM,
∵BC=AB,
∴∠CAB=∠ACB,
∵m∥n,
∴∠MAC=∠ACB,∠FAB=∠ABC,
∴∠MAC=∠CAB,
∴∠CAB=∠EMA,
在△AEB和△MEF中,
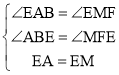 ,
,
∴△AEB≌△MEF(AAS)
∴EF=EB;
(3)EF=BE.
理由如下:如图2,在直线m上截取AN=AB,连接NE,
∵∠ABC=90°,
∴∠CAB=∠ACB=45°,
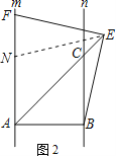
∵m∥n,
∴∠NAE=∠ACB=∠CAB=45°,∠FAB=90°,
在△NAE和△ABE中,
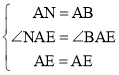 ,
,
∴△NAE≌△ABE(SAS),
∴EN=EB,∠ANE=∠ABE,
∵∠BEF=∠ABC=90°,
∴∠FAB+∠BEF=180°,
∴∠ABE+∠EFA=180°,
∴∠ANE+∠EFA=180°
∵∠ANE+∠ENF=180°,
∴∠ENF=∠EFA,
∴EN=EF,
∴EF=BE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】创新需要每个人的参与,就拿小华来说,为了解决晒衣服的,聪明的他想到了一个好办法,在家宽敞的院内地面![]() 上立两根等长的立柱
上立两根等长的立柱![]() 、
、![]() (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线
(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线![]() ,如图
,如图![]() ,已知立柱
,已知立柱![]() 米,
米, ![]() 米.
米.
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离![]() 为
为![]() 米的位置处用一根垂直于地面的立柱
米的位置处用一根垂直于地面的立柱![]() 撑起绳子 (如图2),使左边抛物线
撑起绳子 (如图2),使左边抛物线![]() 的最低点距
的最低点距![]() 为
为![]() 米,离地面
米,离地面![]() 米,求
米,求![]() 的长.
的长.
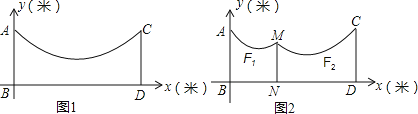
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+6交x轴于A(﹣2,0),B(3,0)两点,交y轴于点C.
(1)求a,b的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为d,求d与t的函数关系式(请求出自变量t的取值范围);
(3)在(2)的条件下,DP与BC交于点F,过点D作DE∥AB交BC于点E,点Q为直线DP上方抛物线上一点,连接AP、PC,若DP=CE,∠QPC=∠APD时,求点Q坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
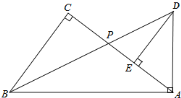
【题目】如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com