
【题目】在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
(1)在下列坐标系中画出这个图案;
(2)若将上述各点的横坐标保持不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连接起来,所得的图案与原图案相比有什么变化?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=36°,AB=AC,∠ABC的平分线BE交AC于E.
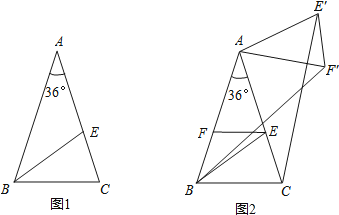
(1)求证:AE=BC;
(2)如图2,过点E作EF∥BC交AB于F,将△AEF绕点A逆时针旋转角α(0°<α<144°)得到△AE′F′,连结CE′、BF′,求证:CE′=BF′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,

(1)求证:ED=FD,
(2)求证:DF⊥DE,
(3)求四边形AFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(1)求m,k的值;
(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=![]() 的图象于点N.
的图象于点N.
①当a=4时,求MN的长;
②若PM>PN,结合图象,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的顶点为点D.
的顶点为点D.
(1)求点D的坐标(用含m的代数式表示);
(2)求函数![]() 的图象与x轴的交点坐标;
的图象与x轴的交点坐标;
(3)若函数![]() 的图象在直线y=m的上方,求m的取值范围.
的图象在直线y=m的上方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的公路![]() 旁有一座山,为方便运输货物现要从公路
旁有一座山,为方便运输货物现要从公路![]() 上的
上的![]() 处开凿隧道修通一条公路到
处开凿隧道修通一条公路到![]() 处,已知点
处,已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() ,与公路上另-停靠站
,与公路上另-停靠站![]() 的距离为
的距离为![]() ,停靠站
,停靠站![]() 之间的距离为
之间的距离为![]() ,且
,且![]()
![]() 求修建的公路
求修建的公路![]() 的长;
的长;
![]() 若公路
若公路![]() 修通后,辆货车从
修通后,辆货车从![]() 处经过
处经过![]() 点到
点到![]() 处的路程是多少?
处的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b+c=0;③a﹣b+c<0;④抛物线的顶点坐标为(2,b);⑤当x<2时,y随x增大而增大.其中结论正确的有______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥三十八中为预防秋季疾病传播,对教室进行“薰药消毒”.已知药物在燃烧释放过程中,室内空气中每立方米含药量![]() (毫克)与燃烧时间
(毫克)与燃烧时间![]() (分钟)之间的关系如图所示(即图中线段
(分钟)之间的关系如图所示(即图中线段![]() 和双曲线在
和双曲线在![]() 点及其右侧的部分),根据图象所示信息,解答下列问题:
点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,![]() 与
与![]() 之间的函数关系式及自变量的取值范围;
之间的函数关系式及自变量的取值范围;
(2)据测定,只有当空气中每立方米的含药量不低于![]() 毫克时,对预防才有作用,且至少持续作用
毫克时,对预防才有作用,且至少持续作用![]() 分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?
分钟以上,才能完全杀死这种病毒,请问这次消毒是否彻底?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合)。若四边形OBCD是平行四边形时,那么![]() 的数量关系是________________.
的数量关系是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com