
【题目】已知:⊙O的半径1,弦AB、AC的长分别为1,![]() ,则△ABC的面积为______.
,则△ABC的面积为______.
【答案】![]() 或
或![]()
【解析】
分两种情况讨论,并作图分析,分别过圆心O向AB、AC作垂线,根据垂径定理和三角函数可求出△ABC的内角度数,然后求出三角形的高,即可求出面积.
①当AB、AC位置如下图所示时,
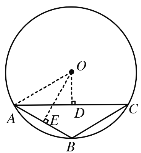
连接OA,过O作OD⊥AC于D,OE⊥AB于E,
由垂径定理可得:AD=![]() AC=
AC=![]() ,AE=
,AE=![]() AB=
AB=![]() ,
,
在Rt△AOD中,  ,
,
∴∠OAD=30°,
在Rt△AOE中,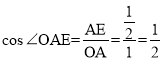 ,
,
∴∠OAE=60°,
∴∠BAC=∠OAE -∠OAD =30°,
∴△ABC中AC边上的高![]() ,
,
∴S△ABC=![]() ,
,
②当AB、AC位置如下图所示时,
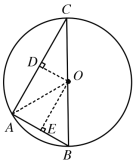
连接OA,过O作OD⊥AC于D,OE⊥AB于E,
同①可得∠OAD=30°,∠OAE=60°,
∴∠BAC=∠OAE +∠OAD =90°
即△ABC为直角三角形,
∴S△ABC=![]() ,
,
综上所述,△ABC的面积为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过A、C、D三点的圆O交AB于点E,连接DE、CE,∠BCE=∠CDE.
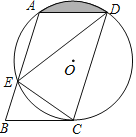
(1)求证:直线BC为圆O的切线;
(2)猜想AD与CE的数量关系,并说明理由;
(3)若BC=2,∠BCE=30°,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )
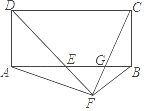
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种流感病毒,有一人患了这种流感,在每轮传染中一人将平均传给![]() 人.
人.
(1)求第一轮后患病的人数;(用含![]() 的代数式表示)
的代数式表示)
(2)在进入第二轮传染之前,有两位患者被及时隔离并治愈,问第二轮传染后总共是否会有21人患病的情况发生,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△OA1B1,顶点A1在双曲线y=![]() (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
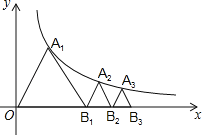
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得落在教学楼第一级台阶上的影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为_____米.
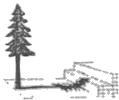
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,⊙O是△ABC的外接圆,点D是![]() 上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
上一点,过点C作⊙O的切线PC,直线PC交BA的延长线于点P,交BD的延长线于点E.
(1)求证:∠PCA=∠PBC;
(2)若PC=8,PA=4,∠ECD=∠PCA,以点C为圆心,半径为5作⊙C,试判断⊙C与直线BD的位置关系.
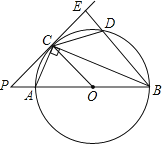
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD中,点E在AD上,△ABE逆时针旋转一定角度后得到△ADF,延长BE交DF于点G,若AE=3,FG=![]() .
.
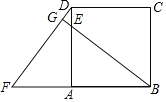
(1)指出旋转中心和旋转角度;
(2)求证:BG⊥DF;
(3)求线段GE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com