
【题目】如图,边长为4的正方形ABCD中,点E在AD上,△ABE逆时针旋转一定角度后得到△ADF,延长BE交DF于点G,若AE=3,FG=![]() .
.
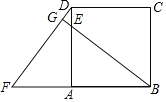
(1)指出旋转中心和旋转角度;
(2)求证:BG⊥DF;
(3)求线段GE的长.
【答案】(1)90°;(2)见解析;(3)![]() ﹣5
﹣5
【解析】
(1)根据图形和已知的△ABE旋转得到△ADF即可得出答案;
(2)由旋转的性质可得∠F=∠AEB,由余角的性质可得结论;
(3)由勾股定理可求BE的长,再由勾股定理可求BG的长,即可求GE的长.
(1)旋转中心是点A,旋转角度是90°;
(2)∵△ADF是由△ABE旋转得到,
∴△ADF≌△ABE,
∴∠F=∠AEB,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AEB+∠ABE=90°,
∴∠F+∠ABE=90°,
∴∠FGB=90°,
∴BG⊥DF;
(3)∵正方形ABCD的边长是4,
∴AB=4,
∴在Rt△ABE中,BE=![]() =5,
=5,
∵AF=AE=3
∴FB=AF+AB=7,
∴在Rt△FBG中,BG=![]() ,
,
∴GE=BG﹣BE=![]() ﹣5.
﹣5.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
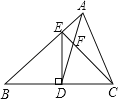
(1)求证:△ABC~△FCD;
(2)若△DEF的面积为2,求△FCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
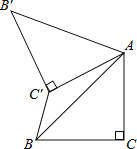
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.
,将△ABC绕点A顺时针方向旋转60°到△ABC的位置,连接C'B.
(1)求∠ABC'的度数;
(2)求C'B的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
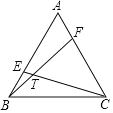
【题目】如图,已知E,F为等边三角形ABC边AB,AC上的两个动点,且AF=BE,连接CE,BF交于点T,若等边三角形ABC的边长为12,则点T运动的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
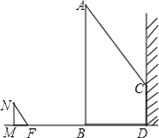
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数的图象与x轴交于同一点,则称这两个函数为一对“x牵手函数”,这个交点为“x牵手点”.
(1)一次函数y=x﹣1与x轴的交点坐标为 ;一次函数y=ax+2与一次函数y=x﹣1为一对“x牵手函数”,则a= ;
(2)已知一对“x牵手函数”:y=ax+1与y=bx﹣1,其中a,b为一元二次方程x2﹣kx+k﹣4=0的两根,求它们的“x牵手点”.
查看答案和解析>>
科目:初中数学 来源: 题型:
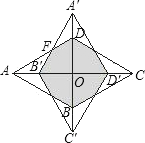
【题目】如图,在菱形ABCD中,∠BAD=60°,对角线AC、BD相交于点O将其绕着点O顺时针旋转90°得到菱形A‘B’C‘D’.若AB=1,则旋转前后两菱形重叠部分图形的周长为__________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com