
����Ŀ��������һ�κ�����ͼ����x�ύ��ͬһ�㣬�������������Ϊһ����xǣ�ֺ��������������Ϊ��xǣ�ֵ�����
��1��һ�κ���y��x��1��x��Ľ�������Ϊ�� ��һ�κ���y��ax+2��һ�κ���y��x��1Ϊһ����xǣ�ֺ���������a���� ��
��2����֪һ����xǣ�ֺ�������y��ax+1��y��bx��1������a��bΪһԪ���η���x2��kx+k��4��0�������������ǵ���xǣ�ֵ�����
���𰸡���1����1��0����a����2����2����xǣ�ֵ㡱Ϊ��![]() ��0����
��0����![]() ��0��.
��0��.
��������
��1������x���ϵ��������������һ�κ���y=x-1��x��Ľ������ꣻ��һ�κ���y=x-1��x��Ľ����������һ�κ���y=ax+2����a��ֵ��
��2��������xǣ�ֺ������Ķ���õ�a+b=0�����ݸ���ϵ���Ĺ�ϵ���k=0���ɵ÷���x2-4=0�����x1=2��x2=-2���ٷ��������������a=2��b=-2������a=-2��b=2���������ۿ������ǵ���xǣ�ֵ�����
�⣺��1����y��0ʱ����x��1��0��
����x��1����һ�κ���y��x��1��x��Ľ�������Ϊ��1��0����
����һ�κ���y��ax+2��һ�κ���y��x��1Ϊһ����xǣ�ֺ�������
����0��a+2��
���a����2��
��2����y��ax+1��y��bx��1Ϊһ����xǣ�ֺ�����
��![]() ��
��
��a+b��0��
��a��bΪx2��kx+k��4��0������
��a+b��k��0��
��x2��4��0��
��x1��2��x2����2��
����a��2��b����2��y��2x+1��y����2x��1����xǣ�ֵ���Ϊ![]() ��
��
����a����2��b��2��y����2x+1��y��2x��1����xǣ�ֵ���Ϊ��![]() ��0 ��
��0 ��
��������������xǣ�ֵ���Ϊ![]() ��
��![]() ��0��
��0��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
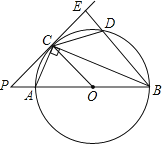
����Ŀ����Rt��ABC�У���ACB��90�㣬��O�ǡ�ABC�����Բ����D��![]() ��һ�㣬����C����O������PC��ֱ��PC��BA���ӳ����ڵ�P����BD���ӳ����ڵ�E��
��һ�㣬����C����O������PC��ֱ��PC��BA���ӳ����ڵ�P����BD���ӳ����ڵ�E��
��1����֤����PCA����PBC��
��2����PC��8��PA��4����ECD����PCA���Ե�CΪԲ�ģ��뾶Ϊ5����C�����жϡ�C��ֱ��BD��λ�ù�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ4��������ABCD�У���E��AD�ϣ���ABE��ʱ����תһ���ǶȺ�õ���ADF���ӳ�BE��DF�ڵ�G����AE��3��FG��![]() ��
��
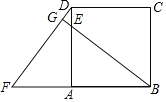
��1��ָ����ת���ĺ���ת�Ƕȣ�
��2����֤��BG��DF��
��3�����߶�GE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
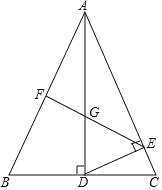
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��AD��BC��D����DE��AC��E��F��AB�е㣬��EF��AD�ڵ�G��
(1)��֤��AD2��ABAE��
(2)��AB��3��AE��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ������������Ŀڴ��У��ֱ��д�С��������ȫ��ͬ��С�����мڴ��е�С���Ϸֱ��������1��2��3��4���ҿڴ��е�С���Ϸֱ��������2��3��4���ȴӼ״�����������һ��С��������Ϊm���ٴ��Ҵ�������һ��С��������Ϊn��
��1�������б�����״ͼ�ķ�����ʾ�����У�m��n�����ܵĽ����
��2����m��n���Ƿ���x2��5x+6��0�Ľ�ʱ����С����ʤ����m��n�����Ƿ���x2��5x+6��0�Ľ�ʱ����С����ʤ������������˭��ʤ�ĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������£�С��ͬѧ���һ����Ϊ![]() ����͵�Ӱ��Ϊ
����͵�Ӱ��Ϊ![]() �ף�
�ף�

![]() ͬһʱ��
ͬһʱ��![]() ����͵�Ӱ��Ϊ________�ף�
����͵�Ӱ��Ϊ________�ף�
![]() ͬһʱ��С���ڲ������ĸ߶�ʱ����������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ�������ڲٳ��ĵ�һ��̨���ϣ�������ڵ�һ��̨���ϵ�Ӱ�ӳ�Ϊ
ͬһʱ��С���ڲ������ĸ߶�ʱ����������Ӱ�Ӳ�ȫ���ڵ����ϣ���һ�������ڲٳ��ĵ�һ��̨���ϣ�������ڵ�һ��̨���ϵ�Ӱ�ӳ�Ϊ![]() �ף���һ��̨�ĸ�Ϊ
�ף���һ��̨�ĸ�Ϊ![]() �ף����ڵ����ϵ�Ӱ�ӳ�Ϊ
�ף����ڵ����ϵ�Ӱ�ӳ�Ϊ![]() �ף������ĸ߶�Ϊ________�ף�
�ף������ĸ߶�Ϊ________�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���֣�Բ�ڽ��ı��εĶԽ� .
��ͼ�٣��ı���![]() ��
��![]() ���ڽ��ı��Σ���
���ڽ��ı��Σ���![]() ����
����![]()
![]() .
.
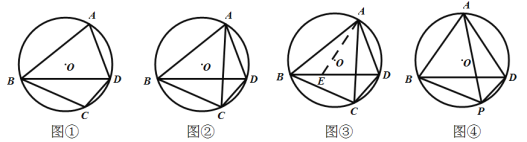
�����ⴴ�£�Բ�ڽ��ı��εı�������������
��ͼ�ڣ�ij��ѧ��ȤС����������о����֣�![]()
֤������ͼ�ۣ���![]() ����
����![]() �ڵ�
�ڵ�![]() .
.
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ���밴���ǵ�˼·�������֤����
���밴���ǵ�˼·�������֤����
��Ӧ��Ǩ�ƣ���ͼ�ܣ���֪�ȱ�![]() ���Բ
���Բ![]() ����
����![]() Ϊ
Ϊ![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
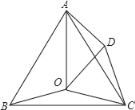
����Ŀ����ͼ����O�ǵȱ�������ABC�ڵ�һ�㣬��BOC��150�㣬����BOC�Ƶ�C��˳ʱ����ת�õ���ADC������OD��OA��
��1�����ODC�Ķ�����
��2����OB��2��OC��3����AO�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2011���ݰ�˳��16��4�֣���ͼ����Rt��ABC�У���C=90����BC=6cm��AC=8cm����ͼ����ʾ��������BCD��BD�۵���ʹ��C����AB�ߵ�C���㣬��ô��ADC��������� ��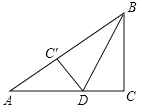
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com