
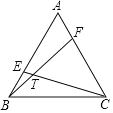
【题目】如图,已知E,F为等边三角形ABC边AB,AC上的两个动点,且AF=BE,连接CE,BF交于点T,若等边三角形ABC的边长为12,则点T运动的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
证明△ABF≌△BCE(SAS),推出∠ABF=∠BCE,推出∠FTC=∠TBC+∠TCB=∠TBC+∠ABF=60°,推出∠BTC=120°,因为BC=12是定值,推出点T的运动轨迹是![]() ,设圆心为O,连接OB,OC,作OH⊥BC,求出圆心角,半径,即可解决问题.
,设圆心为O,连接OB,OC,作OH⊥BC,求出圆心角,半径,即可解决问题.
如图,

∵△ABC是等边三角形,
∴AB=BC,∠A=∠CBE=60°,
∵AF=BE,
∴△ABF≌△BCE(SAS),
∴∠ABF=∠BCE,
∴∠FTC=∠TBC+∠TCB=∠TBC+∠ABF=60°,
∴∠BTC=120°,
∵BC=12是定值,
∴点T的运动轨迹是![]() ,设圆心为O,连接OB,OC,作OH⊥BC,
,设圆心为O,连接OB,OC,作OH⊥BC,
∵OB=OC,OH⊥BC,
∴BH=CH=6,
∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴OB=![]() =4
=4![]() ,
,
∴![]() 的长=
的长=![]() =
=![]() ,
,
故选:D.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
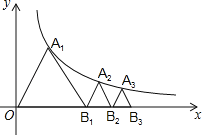
【题目】如图,已知等边△OA1B1,顶点A1在双曲线y=![]() (x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
(x>0)上,点B1的坐标为(2,0).过B1作B1A2∥OA1交双曲线于点A2,过A2作A2B2∥A1B1交x轴于点B2,得到第二个等边△B1A2B2;过B2作B2A3∥B1A2交双曲线于点A3,过A3作A3B3∥A2B2交x轴于点B3,得到第三个等边△B2A3B3;以此类推,…,则点B6的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察发现;如图1,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,过
上,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() .填空:
.填空:
①![]() 与
与![]() 是否相似? (直接回答)______;
是否相似? (直接回答)______;
②![]() _______;
_______; ![]() .
.
(2)拓展探究:将![]() 绕顶点
绕顶点![]() 旋转到图2所示的位置,猜想
旋转到图2所示的位置,猜想![]() 与
与![]() 是否相似?若不相似,说明理由;若相似,请证明.
是否相似?若不相似,说明理由;若相似,请证明.
(3)迁移应用:将![]() 绕顶点
绕顶点![]() 旋转到点
旋转到点![]() 在同一条直线上时,直接写出线段
在同一条直线上时,直接写出线段![]() 的长是 .
的长是 .
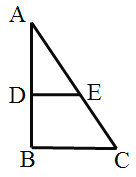
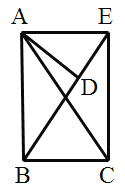
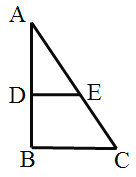
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某货车销售公司,分别试销售两种型号货车各一个月,并从中选择一种长期销售,设每月销售量为x辆若销售甲型货车,每月销售的利润为y1(万元),已知每辆甲型货车的利润为(m+6)万元,(m是常数,9≤m≤11),每月还需支出其他费用8万元,受条件限制每月最多能销售甲型货车25辆;若销售乙型货车,每月的利润y2(万元)与x的函数关系式为y2=ax2+bx-25,且当x=10时,y2=20,当x=20时,y2=55,受条件限制每月最多能销售乙型货车40辆.
(1)分别求出y1、y2与x的函数关系式,并确定x的取值范范围;
(2)分别求出销售这两种货车的最大月利润;(最大利润能求值的求值,不能求值的用式子表示)
(3)为获得最大月利润,该公司应该选择销售哪种货车?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD中,点E在AD上,△ABE逆时针旋转一定角度后得到△ADF,延长BE交DF于点G,若AE=3,FG=![]() .
.
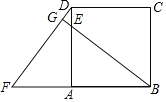
(1)指出旋转中心和旋转角度;
(2)求证:BG⊥DF;
(3)求线段GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.

(1)当∠BAC=30时,求△ABC的面积;
(2)当DE=8时,求线段EF的长;
(3)在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.
(1)请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2)若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com