
【题目】如图,平面直角坐标系,抛物线![]() (
(![]() ,
,![]() )与
)与![]() 轴交于A、B两点(A在B左侧),与
轴交于A、B两点(A在B左侧),与![]() 轴交于点C,过抛物线的顶点P且与
轴交于点C,过抛物线的顶点P且与![]() 轴平行的直线
轴平行的直线![]() 交BC于点D,且满足BD:CD=3:2,
交BC于点D,且满足BD:CD=3:2,
(1)若∠ACB=90°,求抛物线解析式;
(2)问OC和DP能否相等?若能,求出抛物线解析式,若不能,说明理由.
【答案】(1)![]() ;(2)不能,理由见解析
;(2)不能,理由见解析
【解析】
(1)根据平行线分线段成比例定理结合对称轴的性质得到![]() ,BE=AE,设BE=AE=3m,则OE=2m,AO=m,再证得△AOC∽△COB,根据对应边成比例,列式可求得
,BE=AE,设BE=AE=3m,则OE=2m,AO=m,再证得△AOC∽△COB,根据对应边成比例,列式可求得![]() 的值,即求得点A、B的坐标,利用待定系数法即可求解;
的值,即求得点A、B的坐标,利用待定系数法即可求解;
(2)由(1)知:A(-m,0),B(5m,0),可求得抛物线的解析式为![]() ,则顶点为P(2m,-9),即EP=9,根据△BDE∽△BCO求得DE的长,DP的长,从而证明OC和DP不可能相等.
,则顶点为P(2m,-9),即EP=9,根据△BDE∽△BCO求得DE的长,DP的长,从而证明OC和DP不可能相等.
(1)设直线![]() 交x轴于点E,
交x轴于点E,
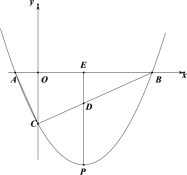
∵直线![]() ∥
∥![]() 轴,即DE∥OC,
轴,即DE∥OC,
∴![]() ,
,
∵直线![]() 经过顶点P,
经过顶点P,
∴直线![]() 是抛物线的对称轴,
是抛物线的对称轴,
∴BE=AE,
设BE=AE=3m,则OE=2m,AO=m,
当∠ACB=90°时,
∵∠ACO+∠BCO=90![]() ,∠ACO+∠CAO=90
,∠ACO+∠CAO=90![]() ,
,
∴∠CAO=∠BCO,
∴△AOC∽△COB,
∴![]() ,
,
故OC=AO·BO,即5=m·5m,
解得![]() 或
或![]() (舍去),
(舍去),
∴A(![]() ,0),B(
,0),B(![]() ,0),
,0),
将A,B坐标代入![]() ,
,
得: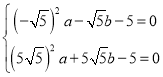 ,
,
解得![]() ,
,
故二次函数的解析式为![]() ;
;
(2)由(1)知:A(-m,0),B(5m,0),
设二次函数的解析式为![]() ,
,
将C(0,-5)代入得:![]() ,
,
解得![]() ,
,
∴![]() ,
,
故P(2m,-9),即EP=9,
∵DE∥OC,
∴△BDE∽△BCO,
∴![]() ,且OC=5,
,且OC=5,
∵BD:CD=3:2,
∴DE=![]() ,
,
∴PD=9-3=6,
∵5≠6,
∴OC≠DP,
故OC和DP不可能相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校开展研学旅行活动,准备去的研学基地有A(曲阜)、B(梁山)、C(汶上),D(泗水),每位学生只能选去一个地方,王老师对本全体同学选取的研学基地情况进行调查统计,绘制了两幅不完整的统计图(如图所示).
(1)求该班的总入数,并补全条形统计图.
(2)求D(泗水)所在扇形的圆心角度数;
(3)该班班委4人中,1人选去曲阜,2人选去梁山,1人选去汶上,王老师要从这4人中随机抽取2人了解他们对研学基地的看法,请你用列表或画树状图的方法,求所抽取的2人中恰好有1人选去曲阜,1人选去梁山的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天,求甲、乙两厂每天能生产口罩多少万只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有A、B、C三地,甲、乙两车同时从A地出发,分别匀速前往B地、C地,甲车到达B地停留一段时间后原速原路返回,乙车到达C地后立即原速原路返回,乙车比甲车早1小时返回A地,甲、乙两车各自行驶的路程y(千米)与时间x(时)(从两车出发时开始计时)之间的函数图象如图所示.
(1)甲车到达B地停留的时长为 小时.
(2)求甲车返回A地途中y与x之间的函数关系式.
(3)直接写出两车在途中相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发之后,全国许多省市对湖北各地进行了援助,广州市某医疗队备好医疗防护物资迅速援助武汉.第一批医疗队员乘坐高铁从广州出发,2.5小时后,第二批医疗队员乘坐飞机从广州出发,两批队员刚好同时到达武汉.已知广州到武汉的飞行距离为800千米,高铁路程为飞行距离的![]() 倍.
倍.
(1)求广州到武汉的高铁路程;
(2)若飞机速度与高铁速度之比为5:2,求飞机和高铁的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场打算在年前用30000元购进一批彩灯进行销售,由于进货厂家促销,实际可以以8折的价格购进这批彩灯,结果可以比计划多购进了100盏彩灯.
(1)该商场购进这种彩灯的实际进价为多少元?
(2)该商场打算在实际进价的基础上,每盏灯加价50%的销售,但可能会面临滞销,因此将有20%的彩灯需要降价,以5折出售,该商场要想获利不低于15000元,应至少在购进这种彩灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
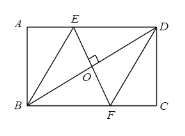
【题目】如图,在矩形ABCD中,AB=3,做BD的垂直平分线E,F,分别与AD、BC交于点E、F,连接BE,DF,若EF=AE+FC,则边BC的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com