
����Ŀ�����Ķ����⣩������������A��B����ʾ�����ֱ�Ϊa��b������
��A��B������е��ʾ����Ϊ![]() ��
��
�ڵ�b��aʱ��A��B�����ľ���ΪAB��b��a��
��������⣩����������A��B����ʾ�����ֱ�Ϊa��b��������|a+2|+��b��8��2020��0
��1�����A��B������е�C��ʾ������
��2����D��ԭ��O����������˶�������2����D��A��ľ����ǵ�D��C������2�������D���˶��ٶ���ÿ����ٸ���λ���ȣ�
����ѧ˼������3����E��ÿ��1����λ���ٶȴ�ԭ��O���������˶���ͬʱ����M�ӵ�A������ÿ��7����λ���ٶ������˶�����N�ӵ�B��������ÿ��10����λ���ٶ������˶���P��Q�ֱ�ΪME��ON���е㣮˼�������˶������У�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
���𰸡���1��A��B������е�C��ʾ������3����2����D���˶��ٶ���ÿ��![]() ����λ���ȣ���ÿ��4����λ���ȣ���3��
����λ���ȣ���ÿ��4����λ���ȣ���3��![]() =2����ֵ�������ɼ�����.
=2����ֵ�������ɼ�����.
��������
��1���ֱ����a��b��ֵ��Ȼ������е�C��ֵ��
��2����������ۣ�����D�˶�����C��ߺ�C�ұ�ʱ���ó���һ����Cֵ��
��3�����˶�ʱ��Ϊt�����E��Ӧ������t����M��Ӧ�����ǩ�2��7t����N��Ӧ������8+10t��![]()
��1����|a+2|+��b��8��2020��0
��a����2��b��8��
��A��B������е�C��ʾ�����ǣ�![]() ��
��
��2�����D���˶��ٶ�Ϊv��
�ٵ���D�˶�����C���ʱ�������⣬��2v������2����2��3��2v����
��֮��![]() ��
��
�ڵ���D�˶�����C�ұ�ʱ�������⣬��2v������2����2��2v��3����
��֮��v��4��
���D���˶��ٶ���ÿ��![]() ����λ���ȣ���ÿ��4����λ���ȣ�
����λ���ȣ���ÿ��4����λ���ȣ�
��3�����˶�ʱ��Ϊt�����E��Ӧ������t����M��Ӧ�����ǩ�2��7t����N��Ӧ������8+10t��
��P��ME���е㣬
��P���Ӧ������![]() ��
��
�֡�Q��ON���е㣬
��Q���Ӧ������![]() ��
��
��MN����8+10t��������2��7t����10+17t��OE��tPQ����4+5t��������1��3t����5+8t��
��![]() ����ֵ��.
����ֵ��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ƻ�����![]() ���ֲ�Ʒ��60�����蹺��ס������ֲ���.����һ��
���ֲ�Ʒ��60�����蹺��ס������ֲ���.����һ��![]() ��Ʒ����ֲ���4ǧ�ˣ�����һ��
��Ʒ����ֲ���4ǧ�ˣ�����һ��![]() ��Ʒ��ס������ֲ��ϸ�3ǧ��.�����㣬����ס������ֲ��ϸ�1ǧ�˹����ʽ�60Ԫ��������ֲ���2ǧ�˺����ֲ���3ǧ�˹����ʽ�155Ԫ.
��Ʒ��ס������ֲ��ϸ�3ǧ��.�����㣬����ס������ֲ��ϸ�1ǧ�˹����ʽ�60Ԫ��������ֲ���2ǧ�˺����ֲ���3ǧ�˹����ʽ�155Ԫ.
��1���ס������ֲ���ÿǧ�˷ֱ��Ƕ���Ԫ��
��2���ֹ������ڹ���ס������ֲ��ϵ��ʽ���9900Ԫ��������![]() ��Ʒ������38�����ʷ������������������������ļ��֣�
��Ʒ������38�����ʷ������������������������ļ��֣�
��3���ڣ�2���������£�������һ��![]() ��Ʒ��ӹ���40Ԫ������һ��
��Ʒ��ӹ���40Ԫ������һ��![]() ��Ʒ��ӹ���50Ԫ��Ӧѡ����������������ʹ������60����Ʒ�ijɱ���ͣ��ɱ�=���Ϸ�+�ӹ��ѣ���
��Ʒ��ӹ���50Ԫ��Ӧѡ����������������ʹ������60����Ʒ�ijɱ���ͣ��ɱ�=���Ϸ�+�ӹ��ѣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷�ֹˮ����ʧ��ij�忪չ�̻���ɽ����ƻ�����������ʹ�����̻����������360��ƽ���ף���2014�����ʼʵʩ��ʵ��ÿ���̻������ԭ�ƻ���1.6������������ǰ4�����������ʵ��ÿ���̻����������ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵ���������ABC�У�AB��AC��10��BC��12��DΪBC���ϵ�����һ�㣬����D�ֱ���DE��AB��DF��AC������ֱ�ΪE��F����DE��DF��______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��B�������϶�Ӧ�����ֱ���+2����6��ʾ��P�������ϵ�һ�����㣮
![]()
��1��������A��B����ľ���Ϊ�� ��
��2����P������PB��2PAʱ����P���ʾ������
��3����һö���ӷ���������k0�㣬��һ����k��������2����λ��k1���ڶ�����k1��������4����λ��k2����������k2��������6����λ��k3�����IJ���k3��������8����λ��k4��
�������6�����������������k6�㣬��k6��ʾ������12����ko��ֵ�Ƕ��٣�
�����������1002�����������������ϵĵ�k1002�����k1002����ʾ������1998����ôk0����ʾ�������� ����ֱ��д�𰸣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ֽ������һ���ᣬ��ͼ��ʾ����OΪԭ�㣬��A1��A2��A3�����ֱ��ʾ������1��2��3��������B1��B2��B3�����ֱ��ʾ��������1����2����3������
![]()
��1���۵�ֽ�棺
������A1���B1�غϣ����B2����� ���غϣ�
������B1���A2�غϣ����A5���������� ����Ӧ�ĵ��غϣ�
������B1��A3�غϣ��������ϵ�M��N��M��N����ࣩ����֮��ľ���Ϊ9����M��N���㾭�۵����غ�ʱ����M��N�����ʾ���������ֱ����� ������ ����
��2����չ˼����
��A�������ϱ�ʾ��������Ϊa����|a|��ʾ��A��ԭ��O�ľ��룮
��|a��1|�DZ�ʾ��A������ ���ľ��룻
����|a��1|��3����������a���� ����
����|a��1|+|a+2|��5����������a���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������εĶ������α��Ϊ1��2��3��4��5������ijһ���㿪ʼ����������εı�˳ʱ�뷽�����ߣ������ŵ������Ǽ����������߳�����������߷�Ϊһ������λ�����磺С���ڱ��Ϊ3�Ķ�����ʱ����ô��Ӧ��3���߳�������3��4��5��1Ϊ��һ������λ������ʱ��������Ϊ1�Ķ��㣻Ȼ���1��2Ϊ�ڶ�������λ������С��ӱ��Ϊ2�Ķ��㿪ʼ����15������λ����������������ı��Ϊ__��
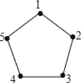
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
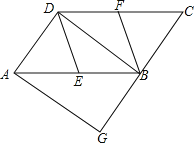
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬��A����AG��DB����CB���ӳ����ڵ�G��
��1����֤��DE��BF��
��2������G=90����֤���ı���DEBF�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ������A��![]() ��0����B��0��2�������B2018������Ϊ��������
��0����B��0��2�������B2018��������������

A. ��6048��0��B. ��6054��0��C. ��6048��2��D. ��6054��2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com