
【题目】探究与发现:
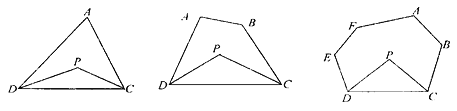
图1 图2 图3
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
【答案】(1)∠P=90°+![]() ∠A (2) ∠P=
∠A (2) ∠P=![]() (∠A+∠B)(3)∠P=
(∠A+∠B)(3)∠P=![]() (∠A+∠B+∠E+∠F)-180°
(∠A+∠B+∠E+∠F)-180°
【解析】试题分析:探究一:根据角平分线的定义可得∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,然后根据三角形内角和定理列式整理即可得解;
∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
试题解析:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠ACD,
∠ACD,
=180°-![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°-![]() (180°-∠A),
(180°-∠A),
=90°+![]() ∠A;
∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠BCD,
∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠BCD,
∠BCD,
=180°-![]() (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°-![]() (360°-∠A-∠B),
(360°-∠A-∠B),
=![]() (∠A+∠B);
(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6-2)180°=720°,
∵DP、CP分别平分∠ADC和∠ACD,
∴∠P=![]() ∠ADC,∠PCD=
∠ADC,∠PCD=![]() ∠ACD,
∠ACD,
∴∠P=180°-∠PDC-∠PCD,
=180°-![]() ∠ADC-
∠ADC-![]() ∠ACD,
∠ACD,
=180°-![]() (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°-![]() (720°-∠A-∠B-∠E-∠F),
(720°-∠A-∠B-∠E-∠F),
=![]() (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P=![]() (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.
考点: 1.多边形内角与外角;2.三角形内角和定理.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.
△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
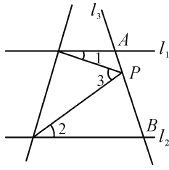
【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南充某制衣厂现有22名制作服装的工人,每天都制作某种品牌的衬衫和裤子,每人每天可制作这种衬衫3件或裤子5条。
(1)若该厂要求每天制作的衬衫和裤子配套,一件衬衫配两条裤子,则应各安排多少人分别制作衬衫和裤子?
(2)已知制作一件衬衫可获得利润30元,制作一条裤子可获得利润16元,在(1)的条件下,求该厂每天制作衬衫和裤子所获得的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D(D不与A、B重合),当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC.此时BE与DC有怎样的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中, ∠ACB=90°,CD⊥AB于D.
(1)请直接写出图中所有的相似三角形 (2)你能得出CD2=AD·DB吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)(1)阅读理解:
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=![]() AE2;④S△ABC=4S△ADF.其中正确的有___________.
AE2;④S△ABC=4S△ADF.其中正确的有___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四个相同的小长方形,然后按图②的方式拼成一个正方形.
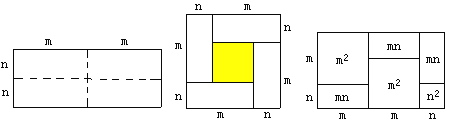
图① 图② 图③
(1)你认为图②中的阴影部分的正方形的边长等于________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①: ;
方法②: ;
(3)请你观察图②,利用图形的面积写出![]() 、
、![]() ,
, ![]() 这三个代数式之间的等量关系: ;
这三个代数式之间的等量关系: ;
(4)根据(3)中的结论,若![]() ,
, ![]() ,则
,则![]() ;
;
(5)有许多代数恒等式可以用图形的面积来表示.
如图③,它表示了![]()
![]() .
.
试画出一个几何图形,使它的面积能表示: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com