
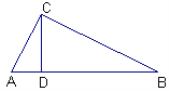
【题目】如图在Rt△ABC中, ∠ACB=90°,CD⊥AB于D.
(1)请直接写出图中所有的相似三角形 (2)你能得出CD2=AD·DB吗?为什么?
【答案】详见解析.
【解析】试题分析:
(1)由已知条件易证:∠ADC=∠BDC=∠ACB=90°,∠B=∠ACD,∠A=∠BCD,因此可得:△ABC∽△ACD, △ABC∽△CBD,△ACD∽△CBD;
(2)由△ACD∽△CBD可得:AD:CD=CD:BD,即CD2=AD![]() BD.
BD.
试题解析:
(1)∵Rt△ABC中, ∠ACB=90°,CD⊥AB于D,
∴∠ADC=∠BDC=∠ACB=90°,
∴∠ACD+∠A=90°,∠A+∠B=90°,∠ACD+∠BCD=90°,
∴∠ACD=∠B,∠A=∠BCD,
∴△ABC∽△ACD, △ABC∽△CBD,△ACD∽△CBD;
(2)能得出CD2=AD·DB,理由如下:
∵△ACD∽△CBD,
∴AD:CD=CD:BD,
∴CD2=AD![]() BD.
BD.


科目:初中数学 来源: 题型:
【题目】实验与探究:
(![]() )由图观察易知
)由图观察易知![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,请在图中分别标明
,请在图中分别标明![]() 、
、![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 、
、![]() 的位置,并写出他们的坐标:
的位置,并写出他们的坐标:![]() __________、
__________、![]() __________.
__________.
归纳与发现:
(![]() )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为__________(不必证明).
的坐标为__________(不必证明).
运用与拓广:
(![]() )已知两点
)已知两点![]() 、
、![]() ,试在直线
,试在直线![]() 上确定一点
上确定一点![]() ,使点
,使点![]() 到
到![]() 、
、![]() 两点的距离之和最小,并求出
两点的距离之和最小,并求出![]() 点坐标.
点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A在四边形BCDE的外部时,记∠AEB为∠1,∠ADC为∠2,则∠A、∠1与∠2的数量关系,结论正确的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(x﹣1)(x99+x98+…+…+x+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手.然后归纳出一些方法.
(1)分别化简下列各式:
(x﹣1)(x+1)= ;
(x﹣1)(x2+x+1)= ;
(x﹣1)(x3+x2+x+1)= ;
…
(x﹣1)(x99+x98+…+x+1)= .
(2)请你利用上面的结论计算:
299+298+…+2+1
399+398+…+3+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
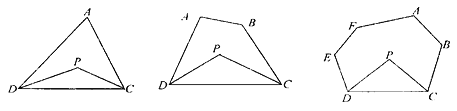
图1 图2 图3
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,
试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,D为BC上一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)若∠BAD=20°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读教科书情况统计图表
类别 | 人数 | 占总人数比例 |
重视 | a | b |
一般 | 57 | 0.285 |
不重视 | c | 0.36 |
说不清楚 | 9 | 0.045 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系.

(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系;
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度a,得到如图2、如图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com