
已知关于x的一元二次方程kx2+(3k+1)x+3=0(k≠)。
(1)求证:无论k取何值,方程总有两个实数根;
(2)若二次函数y= kx2+(3k+1)x+3的图象与x轴两个交点的横坐标均为整数,且k为整数,求k的值。
(1)证明见解析;(2)整数k为±1.
【解析】
试题分析:(1)先计算判别式得值得到△=(3k+1)2-4k×3=(3k-1)2,然后根据非负数的性质得到△≥0,则根据判别式的意义即可得到结论;
(2)先由求根公式得到kx2+(3k+1)x+3=0(k≠0)的解为x1=-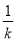 ,x2=-3,则二次函数y=kx2+(3k+1)x+3的图象与x轴两个交点的横坐标分别为-
,x2=-3,则二次函数y=kx2+(3k+1)x+3的图象与x轴两个交点的横坐标分别为-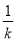 和-3,然后根据整数的整除性可确定整数k的值.
和-3,然后根据整数的整除性可确定整数k的值.
试题解析:(1)证明:△=(3k+1)2-4k×3
=(3k-1)2,
∵(3k-1)2,≥0,
∴△≥0,
∴无论k取何值,方程总有两个实数根;
(2)【解析】
kx2+(3k+1)x+3=0(k≠0)
x=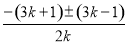 ,
,
x1=-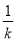 ,x2=-3,
,x2=-3,
所以二次函数y=kx2+(3k+1)x+3的图象与x轴两个交点的横坐标分别为-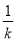 和-3,
和-3,
根据题意得-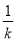 为整数,
为整数,
所以整数k为±1.
考点:1.根的判别式;2.抛物线与x轴的交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:选择题
如图,AB是⊙O的直径,弦CD交AB于点E,∠BAC= ∠BOD,若tan∠BOD=
∠BOD,若tan∠BOD= ,则tan∠BAC=( )
,则tan∠BAC=( )

A.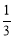 B.
B. C.
C.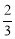 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:选择题
对于四条线段a、b、c、d,如果ab=cd,那么( ).
A. =
= B.
B.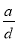 =
= C.
C. =
= D.
D. =
=
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市永定丰田片区九年级上学期第三次月考数学试卷(解析版) 题型:解答题
设点A的坐标(x,y),其中横坐标x可取-1,2,纵坐标y可取-1,1,2。
(1)求出点A的坐标的所有等可能结果(用树形图或列表法求解);
(2)求点A与点B(1,-1)关于原点对称的概率。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市永定丰田片区九年级上学期第三次月考数学试卷(解析版) 题型:填空题
如果扇形的圆心角为120°,半径为3cm,那么扇形的面积是 cm2,弧长 cm。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年云南省九年级11月月考数学试卷(解析版) 题型:解答题
在正方形网格中建立如图所示的平面直角坐标系,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题。
(1)画出△ABC关于 轴对称的△A1B1C1。
轴对称的△A1B1C1。
(2)画出△ABC关于原点对称的△A2B2C2。
(3)将△ABC绕点B逆时针旋转900,画出旋转后的A3BC3。
(4)求△A1A2A3的面积。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省景洪市七年级11月月考数学试卷(解析版) 题型:解答题
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为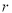 米,广场长为
米,广场长为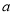 米,宽为
米,宽为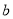 米。
米。

(1)请列式表示广场空地的面积;
(2)若休闲广场的长为400米,宽为100米,圆形花坛的半径为10米,求广场空地的面积(计算结果保留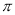 )。
)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com