
分析 根据已知条件可设此多项式为M建立等式解得即可.
解答 解:设这个多项式为M,
则M=$\frac{1}{3}$(x2+x-5)-$\frac{1}{3}$(-x2-x-5)
=$\frac{1}{3}$x2+$\frac{1}{3}$x-$\frac{5}{3}$+$\frac{1}{3}$x2+$\frac{1}{3}$x+$\frac{5}{3}$
=$\frac{2}{3}$x2+$\frac{2}{3}$x.
故答案为:$\frac{2}{3}$x2+$\frac{2}{3}$x
点评 本题考查了整式的加减,熟记去括号法则:--得+,-+得-,++得+,+-得-;及熟练运用合并同类项的法则:字母和字母的指数不变,只把系数相加减.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长NE=2m,试确定小明离路灯CD的距离.
如图,在宽为24m的马路两侧各竖立两根相同高度的灯杆AB、CD.当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长NE=2m,试确定小明离路灯CD的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
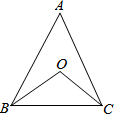 如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 2α° | B. | (α+60)° | C. | (α+90)° | D. | ($\frac{1}{2}$α+90)° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com