
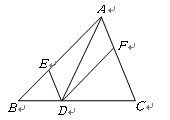
【题目】如图,在![]() 中,点D、E、F分别在边
中,点D、E、F分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() .下列四种说法:
.下列四种说法:
①四边形![]() 是平行四边形;②如果
是平行四边形;②如果![]() ,那么四边形
,那么四边形![]() 是矩形;
是矩形;
③如果![]() 平分
平分![]() ,那么四边形
,那么四边形![]() 是菱形;
是菱形;
④如果![]() 且
且![]() ,那么四边形
,那么四边形![]() 是菱形.
是菱形.
其中,正确的有 .(只填写序号)
科目:初中数学 来源: 题型:
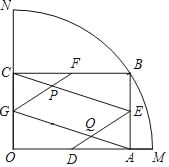
【题目】如图,扇形OMN的半径为1,圆心角为90°,点B是![]() 上一动点,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
(1)当点B移动到使AB:OA=![]() :3时,求
:3时,求![]() 的长;
的长;
(2)当点B移动到使四边形EPGQ为矩形时,求AM的长.
(3)连接PQ,试说明3PQ2+OA2是定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.

定理证明:请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.
定理应用:
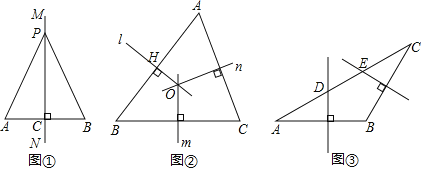
(2)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的垂直平分线,直线
的垂直平分线,直线![]() 、
、![]() 的交点为
的交点为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() .求证:
.求证:![]() .
.
(3)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:△OAB.
求作:⊙O,使⊙O与△OAB的边AB相切.

小明的作法如下:
如图,①取线段OB的中点M;以M为圆心,MO为半径作⊙M,与边AB交于点C;
②以O为圆心,OC为半径作⊙O;
所以,⊙O就是所求作的圆.

请回答:这样做的依据是__________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
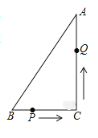
【题目】如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索主要过程:
(1)经过多少时间后,P、Q两点的距离为5![]() cm?
cm?
(2)经过多少时间后,![]() 的面积为15cm2?
的面积为15cm2?
(3)设运动时间为t,用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
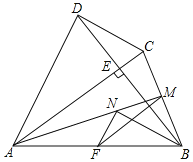
【题目】如图,四边形ABCD中,AC⊥BD交BD于点E,点F、M分别是AB、BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF
求证:(1)BN=![]() MN;
MN;
(2)△MFN∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
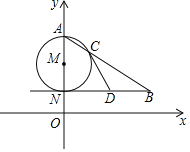
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
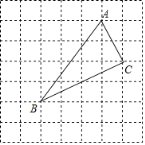
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
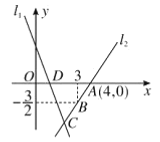
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的和最小,直接写出
的和最小,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com