
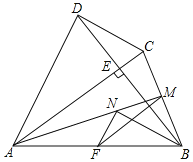
【题目】如图,四边形ABCD中,AC⊥BD交BD于点E,点F、M分别是AB、BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF
求证:(1)BN=![]() MN;
MN;
(2)△MFN∽△BDC.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
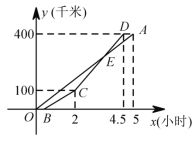
(1)求线段CD对应的函数关系式;
(2)在轿车追上货车后到到达乙地前,何时轿车在货车前30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
(1)求证:AB=BN;
(2)若⊙O半径的长为3,cosB=![]() ,求MA的长.
,求MA的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
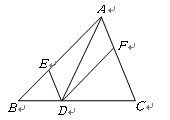
【题目】如图,在![]() 中,点D、E、F分别在边
中,点D、E、F分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() .下列四种说法:
.下列四种说法:
①四边形![]() 是平行四边形;②如果
是平行四边形;②如果![]() ,那么四边形
,那么四边形![]() 是矩形;
是矩形;
③如果![]() 平分
平分![]() ,那么四边形
,那么四边形![]() 是菱形;
是菱形;
④如果![]() 且
且![]() ,那么四边形
,那么四边形![]() 是菱形.
是菱形.
其中,正确的有 .(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
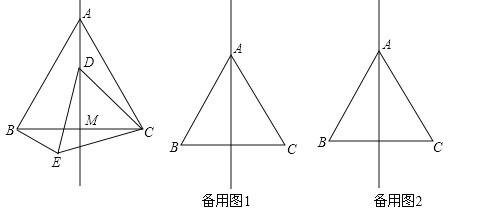
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣![]() x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣
x2+bx+c(a≠0)与x轴交于A(﹣4,0)、B(1,0)两点,与y轴交于C点,对称轴x=﹣![]() ,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
,点N(n,0)是线段AB上的一个动点(N与A、B两点不重合),请回答下列问题:
(1)求出抛物线的解析式,并写出C点的坐标;
(2)试求出当n为何值时,△ANC恰能构成是等腰三角形.
(3)如图2,过N作NF∥BC,与AC相交于D点,连结CN,请问在N点的运动过程中,△CDN的面积是否存在最大值;若存在,试求出该最大面积,若不存在,请说明理由.
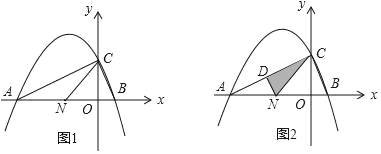
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数 ![]() 的图像分别与 x轴、 y轴交于 A、 B两点,点 C在 y轴上, AC平分
的图像分别与 x轴、 y轴交于 A、 B两点,点 C在 y轴上, AC平分 ![]() .
.
(1) 求点 A、 B的坐标;
(2) 求 ![]() 的面积;
的面积;
(3) 点 P在坐标平面内,且以A、 B、P为顶点的三角形是等腰直角三角形,请你直接写出点 P的坐标.
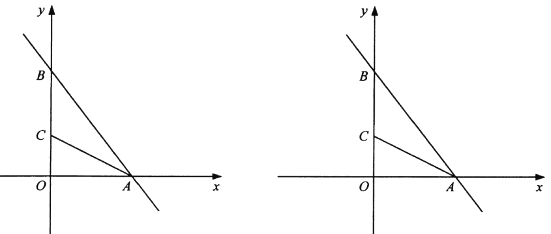
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲、乙仓库共存放某种原料450吨,如果运出甲仓库所存原料的60%,乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将300吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为120元/吨和100元/吨.经协商,从甲仓库到工厂的运价可优惠a元吨(10≤a≤30),从乙仓库到工厂的运价不变,设从甲仓库运m吨原料到工厂,请求出总运费W关于m的函数解析式(不要求写出m的取值范围);
(3)在(2)的条件下,请根据函数的性质说明:随着m的增大,W的变化情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com