
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
(1)求证:AB=BN;
(2)若⊙O半径的长为3,cosB=![]() ,求MA的长.
,求MA的长.

【答案】(1)证明见解析;(2)MA=4.5
【解析】试题分析:
(1)连接OD,可得OD⊥MD,结合BN⊥MD,可得OD∥BN,由此可得∠N=∠ADO;由OA=OD,可得∠OAD=∠ADO,进一步可得∠N=∠OAD,从而就可得到AB=BN;
(2)由(1)中所得的OD∥BN可得∠MOD=∠B,由此可得cos∠MOD=cosB=![]() ,结合OD=OA=3,OM=OA+AM,cos∠MOD=
,结合OD=OA=3,OM=OA+AM,cos∠MOD=![]() 可得
可得![]() ,由此即可解得AM的长.
,由此即可解得AM的长.
试题解析:
(1)连接OD,

∵MD切⊙O于点D,
∴OD⊥MD,
∵BN⊥MC,
∴OD∥BN,
∴∠ADO=∠N,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠N,
∴AB=BN;
(2)∵OD∥BN,
∴∠MOD=∠B,
∴cos∠MOD=cosB=![]() ,
,
∴在Rt△MOD中,cos∠MOD==![]() =
=![]() ,
,
∵OD=OA,MO=MA+OA=3+MA,
∴![]() ,解得:AM=4.5.
,解得:AM=4.5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
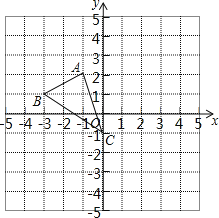
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
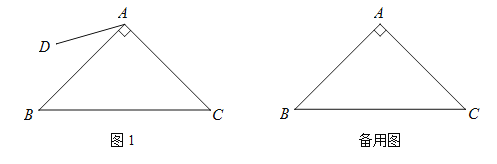
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
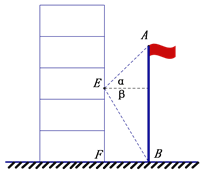
【题目】数学实践课上,同学们分组测量教学楼前国旗杆的高度.小泽同学所在的组先设计了测量方案,然后开始测量了.他们全组分成两个测量队,分别负责室内测量和室外测量(如图).室内测量组来到教室内窗台旁,在点E处测得旗杆顶部A的仰角α为45°,旗杆底部B的俯角β为60°. 室外测量组测得BF的长度为5米.则旗杆AB=______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() 、…
、…![]() 、…,若点
、…,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推进书香校园建设,加强学生课外阅读,某校开展了“走近名家名篇”的主题活动;学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分,如下:
时间(单位: | 频数(人数) | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 15 | 0.30 |
|
| 0.50 |
| 5 |
|

请根据图表信息回答下列问题:
(1)频数分布表中的![]() _________,
_________,![]() ___________;
___________;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校1200名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人在运动时每分钟心跳的次数通常和人的年龄有关,如果用![]() 表示一个人的年龄,用
表示一个人的年龄,用![]() 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么
表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么![]() .
.
![]() 正常情况下,在运动时一个
正常情况下,在运动时一个![]() 岁的人所能承受的每分钟心跳的最高次数是多少?
岁的人所能承受的每分钟心跳的最高次数是多少?
![]() 一个
一个![]() 岁的人运动时
岁的人运动时![]() 秒心跳的次数为
秒心跳的次数为![]() ,请问他有危险吗?为什么?
,请问他有危险吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
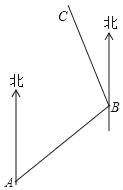
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用![]() 表示距离地面的高度(千米),
表示距离地面的高度(千米),![]() 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出![]() 与
与![]() 的关系式____________________________________;
的关系式____________________________________;
(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com