
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
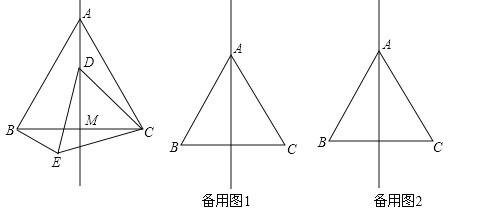
【答案】(1)30°;(2)答案见解析;(3)∠AOB是定值,∠AOB=60°.
【解析】
(1)根据等边三角形的性质可以直接得出结论;
(2)根据等边三角形的性质就可以得出AC=BC,DC=EC,∠ACB=∠DCE=60°,由等式的性质就可以∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
(3)分情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE而有∠CBE=∠CAD=30°而得出结论;当点D在线段MA的延长线上时,如图3,通过得出△ACD≌△BCE同样可以得出结论.
(1)∵△ABC是等边三角形,∴∠BAC=60°.
∵线段AM为BC边上的中线,∴∠CAM![]() ∠BAC,∴∠CAM=∠BAM=30°.
∠BAC,∴∠CAM=∠BAM=30°.
(2)∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD+∠DCB=∠DCB+∠BCE,∴∠ACD=∠BCE.
在△ADC和△BEC中,∵ ,∴△ACD≌△BCE(SAS);
,∴△ACD≌△BCE(SAS);
(3)∠AOB是定值,∠AOB=60°.理由如下:
①当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,又∠ABC=60°,∴∠CBE+∠ABC=60°+30°=90°.
∵△ABC是等边三角形,线段AM为BC边上的中线,∴AM平分∠BAC,即![]() ,∴∠BOA=90°﹣30°=60°.
,∴∠BOA=90°﹣30°=60°.
②当点D在线段AM的延长线上时,如图2.
∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠DCB=∠DCB+∠DCE,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵ ,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD=30°.
,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD=30°.
由(1)得:∠BAM=30°,∴∠BOA=90°﹣30°=60°.
③当点D在线段MA的延长线上时.
∵△ABC与△DEC都是等边三角形,∴AC=BC,CD=CE,∠ACB=∠DCE=60°,∴∠ACD+∠ACE=∠BCE+∠ACE=60°,∴∠ACD=∠BCE.
在△ACD和△BCE中,∵ ,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD.
,∴△ACD≌△BCE(SAS),∴∠CBE=∠CAD.
由(1)得:∠CAM=30°,∴∠CBE=∠CAD=150°,∴∠CBO=30°,∠BAM=30°,∴∠BOA=90°﹣30°=60°.
综上所述:当动点D在直线AM上时,∠AOB是定值,∠AOB=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
![]() 将函数关系式用配方法化为
将函数关系式用配方法化为![]() 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
![]() 在直角坐标系中,画出它的图象.
在直角坐标系中,画出它的图象.
![]() 根据图象说明:当
根据图象说明:当![]() 取何值时,
取何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 当
当![]() 取何值时,
取何值时,![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PO⊥AB,PE是⊙O的切线,交AB的延长线于点C,切点为E,AE交PO于点F.
(1)求证:![]() PEF是等腰三角形;
PEF是等腰三角形;
(2)在图中,作EH⊥AB,垂足为H,作弦BD∥PC,交EH于点G.若EG=5,sinC=![]() ,求直径AB的长.
,求直径AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一笔直的公路连接M,N两地,甲车从M地驶往N地,速度为60km/h,乙车从M地驶往N地,速度为40km/h,丙车从N地驶往M地,速度为80km/h,三辆车同时出发,先到目的地的车停止不动.途中甲车发生故障,于是停车修理了2.5h,修好后立即按原速驶往N地.设甲车行驶的时间为t(h),甲、丙两车之间的距离为S1(km).甲、乙两车离M地的距离为S2(km),S1与t之间的关系如图1所示,S2与t之间的关系如图2所示.根据题中的信息回答下列问题:

(1)①图1中点C的实际意义是 ;
②点B的横坐标是 ;点E的横坐标是 ;点Q的坐标是 ;
(2)请求出图2中线段QR所表示的S2与t之间的关系式;
(3)当甲、乙两车距70km时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图所示的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)64的展开式中第63项的系数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
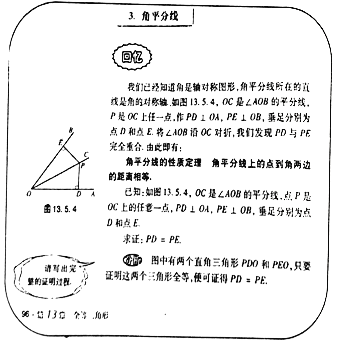

请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数和反比例函数的图象都经过点A(﹣3,﹣3).
(1)求正比例函数和反比例函数的表达式;
(2)把直线OA向上平移后与反比例函数的图象交于点B(﹣6,m),与x轴交于点C,求m的值和直线BC的表达式;
(3)在(2)的条件下,直线BC与y轴交于点D,求以点A,B,D为顶点的三角形的面积;
(4)在(3)的条件下,点A,B,D在二次函数的图象上,试判断该二次函数在第三象限内的图象上是否存在一点E,使四边形OECD的面积S1与四边形OABD的面积S满足:S1=![]() S?若存在,求点E的坐标;若不存在,请说明理由.
S?若存在,求点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则sinB=![]() ,sinC=
,sinC=![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有:![]() ,
,![]() ,所以
,所以![]() .
.
即:在一个三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)自从去年日本政府自主自导“钓鱼岛国有化”闹剧以来,我国政府灵活应对,现如今已对钓鱼岛执行常态化巡逻.某次巡逻中,如图(3),我渔政204船在C处测得A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政204船距钓鱼岛A的距离AB.(结果精确到0.01,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在学习《圆》这一章时,老师给同学们布置了一道尺规作图题:
尺规作图:过圆外一点作圆的切线.
已知:P为⊙O外一点.
求作:经过点P的⊙O的切线.
小敏的作法如下:如图,
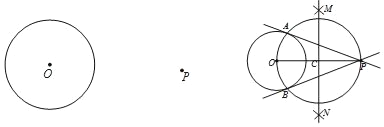
(1)连接OP,作线段OP的垂直平分线MN交OP于点C.
(2)以点C为圆心,CO的长为半径作圆,交⊙O于A,B两点.
(3)作直线PA,PB.
老师认为小敏的作法正确.
请回答:连接OA,OB后,可证∠OAP=∠OBP=90°,其依据是 ;由此可证明直线PA,PB都是⊙O的切线,其依据是 .请写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com