
【题目】如图,AB是⊙O的直径,PO⊥AB,PE是⊙O的切线,交AB的延长线于点C,切点为E,AE交PO于点F.
(1)求证:![]() PEF是等腰三角形;
PEF是等腰三角形;
(2)在图中,作EH⊥AB,垂足为H,作弦BD∥PC,交EH于点G.若EG=5,sinC=![]() ,求直径AB的长.
,求直径AB的长.

【答案】(1)见解析;(2)直径AB的长为20m
【解析】
(1)由切线性质得:OE⊥PC,根据垂直定义和三角形定理可得:∠AEP=∠PFE,根据等角对等边可得结论;
(2)先根据sinC=![]() =
=![]() ,设OH=3x,OE=5x,则EH=4x,OA=OB=5x,由平行线性质得:∠GBH=∠C,
,设OH=3x,OE=5x,则EH=4x,OA=OB=5x,由平行线性质得:∠GBH=∠C,
列式为:![]() =
=![]() ,解方程可得结论.
,解方程可得结论.
(1)证明:∵PE为⊙O的切线,
∴OE⊥PC,
∴∠OEP=90°,
∴∠OEA+∠AEP=90°,
∵OP⊥AC,
∴∠AOF=90°,
∴∠A+∠AFO=90°,
∵∠AFO=∠PFE,
∴∠PFE+∠A=90°,
∵OA=OE,
∴∠A=∠OEA,
∴∠AEP=∠PFE,
∴PE=PF;
∴△PEF是等腰三角形;
(2)解:∵∠C+∠COE=90°,∠COE+∠OEH=90°,
∴∠C=∠OEH,
∵sin∠C=![]() =sin∠OEH=
=sin∠OEH=![]() ,
,
设OH=3x,OE=5x,则EH=4x,OA=OB=5x,
∴BH=OB﹣OH=2x,GH=4x﹣5,
∵BG∥PC,
∴∠GBH=∠C,
∵sin∠C=![]() ,
,
∴tan∠C=![]() =tan∠GBH,
=tan∠GBH,
∴![]() ,x=2,
,x=2,
∴AB=10x=20,
答:直径AB的长为20m.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
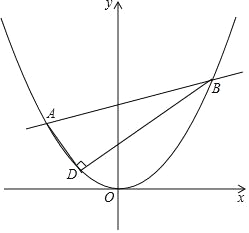
【题目】已知抛物线y=![]() x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
x2,以D(﹣2,1)为直角顶点作该抛物线的内接Rt△ADB(即A.D.B均在抛物线上).直线AB必经过一定点,则该定点坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高为![]() 米的小区超市,超市以上是居民住房,现计划在该楼前面
米的小区超市,超市以上是居民住房,现计划在该楼前面![]() 米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为
米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为![]() .(参考数据在
.(参考数据在![]() ,
,![]() )
)
![]() 中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
![]() 若新建的大楼高
若新建的大楼高![]() 米,则中午时,超市以上的居民住房采光是否受影响,为什么?
米,则中午时,超市以上的居民住房采光是否受影响,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图1和图2中的四边形ABCD都是正方形,△ABE的边长分别为a,b,c,请你从图1到图2,图2到图3的变换过程中,利用几何图形的面积关系,求a,b,c之间的等量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知AE∥BF,AE=BF,A、C、D、B在同一直线上,要使△ADE≌△BCF,可添加的一个条件可以是____________________.(写一个即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,在△ABC外侧作直线CP,点A关于直线CP的对称点为D,连接AD,BD,其中BD交直线CP于点E.
(1)如图1,∠ACP=15°.
①依题意补全图形;
②求∠CBD的度数;
(2)如图2,若45°<∠ACP<90°,直接用等式表示线段AC,DE,BE之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
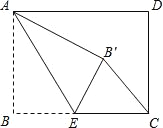
【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
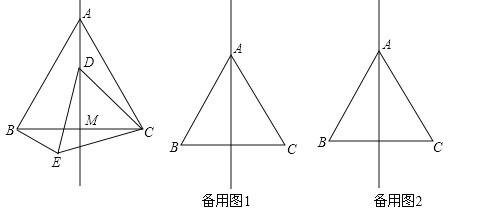
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1).
(1)求一次函数解析式;
(2)判断(3,5)是否在一次函数图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com