
【题目】如图,已知正比例函数和反比例函数的图象都经过点A(﹣3,﹣3).
(1)求正比例函数和反比例函数的表达式;
(2)把直线OA向上平移后与反比例函数的图象交于点B(﹣6,m),与x轴交于点C,求m的值和直线BC的表达式;
(3)在(2)的条件下,直线BC与y轴交于点D,求以点A,B,D为顶点的三角形的面积;
(4)在(3)的条件下,点A,B,D在二次函数的图象上,试判断该二次函数在第三象限内的图象上是否存在一点E,使四边形OECD的面积S1与四边形OABD的面积S满足:S1=![]() S?若存在,求点E的坐标;若不存在,请说明理由.
S?若存在,求点E的坐标;若不存在,请说明理由.

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ;(4)E的坐标是(﹣2,﹣
;(4)E的坐标是(﹣2,﹣![]() ).
).
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)把B(﹣6,m)代入反比例函数解析式即可求出m的值,再根据直线平移的性质即可求直线BC的表达式;
(3)作AM⊥y轴于点M,作BN⊥y轴于点N,根据S四边形ABDM=S梯形ABNM+S△BDN,S△ABD=S四边形ABDM﹣S△ADM即可求解;
(4)设二次函数的解析式是y=ax2+bx+![]() ,然后利用待定系数法求得二次函数的解析式,根据S1=
,然后利用待定系数法求得二次函数的解析式,根据S1=![]() S即可求得S1的值,根据S1=S△OCD+S△OCE列方程求出y0的值,再由E(x0,y0)在二次函数的图象上,即可求得x0的值,进而求得E的坐标.
S即可求得S1的值,根据S1=S△OCD+S△OCE列方程求出y0的值,再由E(x0,y0)在二次函数的图象上,即可求得x0的值,进而求得E的坐标.
解:(1)设正比例函数的解析式是y=kx,代入(﹣3,﹣3),得:﹣3k=﹣3,解得:k=1,
则正比例函数的解析式是:y=x;
设反比例函数的解析式是y=![]() ,把(﹣3,﹣3)代入解析式得:k1=9,
,把(﹣3,﹣3)代入解析式得:k1=9,
则反比例函数的解析式是:y=![]() ;
;
(2)m=![]() =﹣
=﹣![]() ,则点B的坐标是(﹣6,﹣
,则点B的坐标是(﹣6,﹣![]() ),
),
∵y=k3x+b的图象是由y=x平移得到,
∴k3=1,即y=x+b,
故一次函数的解析式是:y=x+![]() ;
;
(3)∵y=x+![]() 的图象交y轴于点D,
的图象交y轴于点D,
∴D的坐标是(0,![]() ),
),
作AM⊥y轴于点M,作BN⊥y轴于点N.
∵A的坐标是(﹣3,﹣3),B的坐标是(6,﹣![]() ),
),
∴M的坐标是(0,﹣3),N的坐标是(0,﹣![]() ).
).
∴OM=3,ON=![]() .
.
则MD=3+![]() =
=![]() ,DN=
,DN=![]() +
+![]() =6,MN=3﹣
=6,MN=3﹣![]() =
=![]() .
.
则S△ADM=![]() ×3×
×3×![]() =
=![]() ,S△BDN=
,S△BDN=![]() ×6×6=18,S梯形ABNM=
×6×6=18,S梯形ABNM=![]() ×(3+6)×
×(3+6)×![]() =
=![]() .
.
则S四边形ABDM=S梯形ABNM+S△BDN=![]() +18=
+18=![]() ,
,
S△ABD=S四边形ABDM﹣S△ADM=![]() ﹣
﹣![]() =
=![]() ;
;
(4)设二次函数的解析式是y=ax2+bx+![]() ,
,
则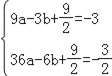 ,
,
解得:![]() ,
,
则这个二次函数的解析式是:y=![]() x2+4x+
x2+4x+![]() ;
;
点C的坐标是(﹣![]() ,0).
,0).
则S=![]() ×6﹣
×6﹣![]() ×6×6﹣
×6×6﹣![]() ×3×
×3×![]() ﹣
﹣![]() ×3×
×3×![]() =45﹣18﹣
=45﹣18﹣![]() ﹣
﹣![]() =
=![]() .
.
假设存在点E(x0,y0),使S1=![]() S=
S=![]() ×
×![]() =
=![]() .
.
∵四边形CDOE的顶点E只能在x轴的下方,
∴y0<0,
∴S1=S△OCD+S△OCE=![]() ×
×![]() ×
×![]() ﹣
﹣![]() ×
×![]() y0=
y0=![]() ﹣
﹣![]() y0,
y0,
∴![]() ﹣
﹣![]() y0=
y0=![]() ,
,
∴y0=﹣![]() ,
,
∵E(x0,y0)在二次函数的图象上,
∴![]() x02+4x0+
x02+4x0+![]() =﹣
=﹣![]() ,
,
解得:x0=﹣2或﹣6.
当x0=﹣6时,点E(﹣6,﹣![]() )与点B重合,这时CDOE不是四边形,故x0=﹣6(舍去).
)与点B重合,这时CDOE不是四边形,故x0=﹣6(舍去).
∴E的坐标是(﹣2,﹣![]() ).
).


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】冬至是一年中太阳光照射最少的日子,如果此时楼房最低层能采到阳光,一年四季整座楼均能受到阳光照射,所以冬至是选房买房时确定阳光照射的最好时机.吴江某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高为![]() 米的小区超市,超市以上是居民住房,现计划在该楼前面
米的小区超市,超市以上是居民住房,现计划在该楼前面![]() 米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为
米处盖一栋新楼,已知吴江地区冬至正午的阳光与水平线夹角大约为![]() .(参考数据在
.(参考数据在![]() ,
,![]() )
)
![]() 中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
中午时,若要使得超市采光不受影响,则新楼的高度不能超过多少米?(结果保留整数)
![]() 若新建的大楼高
若新建的大楼高![]() 米,则中午时,超市以上的居民住房采光是否受影响,为什么?
米,则中午时,超市以上的居民住房采光是否受影响,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
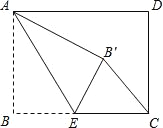
【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
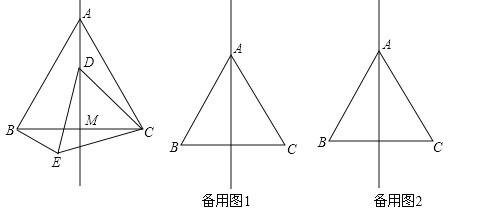
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2![]() ).
).
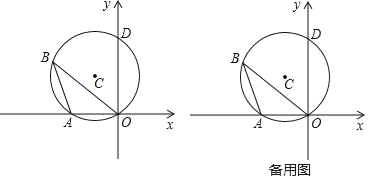
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=![]() (0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()
(1)当8<t≤24时,求P关于t的函数解析式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数解析式;
②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月份,我县教体局由县城老区搬到了新区(海丰16路与棣新4路交叉口),当时某科室需要把相关档案由老区办公楼搬到新区办公楼,甲搬家公司单独工作了3天,完成总量的![]() ;这时为了加快进度,又调来乙搬家公司合干,两队又共同工作了3天,全部搬完档案。假若在工作期间甲、乙两搬家公司各自的工作效率不变,问若单独干完这项工作哪个搬家公司的速度快?(用方程解答)
;这时为了加快进度,又调来乙搬家公司合干,两队又共同工作了3天,全部搬完档案。假若在工作期间甲、乙两搬家公司各自的工作效率不变,问若单独干完这项工作哪个搬家公司的速度快?(用方程解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(﹣2,﹣1).
(1)求一次函数解析式;
(2)判断(3,5)是否在一次函数图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
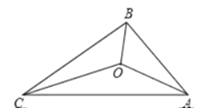
【题目】如图,△ABC的三边AB、BC、CA长分别为30、40、50.其三条角平分线交于点O,则S△ABO :S△BCO :S△CAO =______ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com