
����Ŀ��ijҩ�����۲��Ÿ����г����н�����Ըó�������һ������ԭ��ҩδ����������۽���Ԥ�⣬����������ģ�ͣ����t���¸�ԭ��ҩ����������ΪP����λ���֣���P��t֮�������ͼ��ʾ�ĺ�����ϵ����ͼ���Ǻ���P=![]() ��0��t��8����ͼ�����߶�AB����ϣ����t�������۸�ԭ��ҩÿ�ֵ�ë����ΪQ����λ����Ԫ����Q��t֮���������¹�ϵ��Q=
��0��t��8����ͼ�����߶�AB����ϣ����t�������۸�ԭ��ҩÿ�ֵ�ë����ΪQ����λ����Ԫ����Q��t֮���������¹�ϵ��Q=![]()
��1����8��t��24ʱ����P����t�ĺ�������ʽ��
��2�����t�������۸�ԭ��ҩ����ë����Ϊw����λ����Ԫ��
����w����t�ĺ�������ʽ��
�ڸ�ҩ�����۲��ŷ�����Ϊ��336��w��513���������ڸ�ԭ��ҩ�ɳ������������۵���ë����Χ����˷�Χ����Ӧ����������P����Сֵ�����ֵ��

���𰸡���1��P=t+2����2���ٵ�0��t��8ʱ��w=240����8��t��12ʱ��w=2t2+12t+16����12��t��24ʱ��w=��t2+42t+88���ڴ˷�Χ����Ӧ����������P����СֵΪ12�֣����ֵΪ19�֣�
����������1����8��t��24ʱ��P=kt+b����A��8��10����B��24��26���������ɵ�P=t+2��
��2���ٷ�0��t��8��8��t��12��12��t��24���������������ë����=��������ÿ�ֵ�ë����ɵú�������ʽ��
�����8��t��12��12��t��24ʱ����ë����w������336��w��513������t��ȡֵ��Χ���ٸ���һ�κ��������ʿɵ�P�����ֵ����Сֵ�������ۺϿɵô𰸣�
��1����8��t��24ʱ��P=kt+b��
��A��8��10����B��24��26�����룬�ã�
![]() ��
��
��ã�![]() ��
��
��P=t+2��
��2���ٵ�0��t��8ʱ��w=��2t+8����![]() =240��
=240��
��8��t��12ʱ��w=��2t+8����t+2��=2t2+12t+16��
��12��t��24ʱ��w=��-t+44����t+2��=-t2+42t+88��
�ڵ�8��t��12ʱ��w=2t2+12t+16=2��t+3��2-2��
��8��t��12ʱ��w��t�����������
��2��t+3��2-2=336ʱ������t=10��t=-16���ᣩ��
��t=12ʱ��wȡ�����ֵ�����ֵΪ448��
��ʱ������P=t+2��t=10ʱȡ����Сֵ12����t=12ʱȡ�����ֵ14��
��12��t��24ʱ��w=-t2+42t+88=-��t-21��2+529��
��t=12ʱ��wȡ����Сֵ448��
��-��t-21��2+529=513��t=17��t=25��
�൱12��t��17ʱ��448��w��513��
��ʱP=t+2����СֵΪ14�����ֵΪ19��
���ϣ��˷�Χ����Ӧ����������P����СֵΪ12�֣����ֵΪ19�֣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܹ��б�һ���ı��������ε������ǣ� ��
A. һ��Խ������һ���Խ���ƽ������Խ� B. �Խ�����ƽ��
C. �Խ����ഹֱ����� D. �Խ�������һ���ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��С�������²�����ͼ��
��С�������²�����ͼ��
��1���Ե�OΪԲ�ģ��ʵ���Ϊ�뾶��������OA��D����OB�ڵ�E
��2���ֱ��Ե�D��EΪԲ�ģ�����![]() �ij�Ϊ�뾶������������
�ij�Ϊ�뾶������������![]() ���ڲ��ཻ�ڵ�C
���ڲ��ཻ�ڵ�C
��3��������OC
����������ͼ���裬���н�����ȷ���У� ����
������OC��![]() ��ƽ���ߣ��ڵ�O�͵�C����ֱ��DE�Գƣ�������OC��ֱƽ���߶�DE����
��ƽ���ߣ��ڵ�O�͵�C����ֱ��DE�Գƣ�������OC��ֱƽ���߶�DE����![]() .
.

A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����x��ĶԳƵ�͵�
����x��ĶԳƵ�͵�![]() ����y��ĶԳƵ���ͬ�����
����y��ĶԳƵ���ͬ�����![]() ����x��ԳƵĵ������Ϊ�� ��
����x��ԳƵĵ������Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
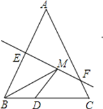
����Ŀ����ͼ��������ABC�ĵױ�BC�ij�Ϊ2cm�������6cm2����AB�Ĵ�ֱƽ����EF��AB�ڵ�E����AC�ڵ�F����DΪBC���ϵ��е㣬MΪ�߶�EF��һ���㣬����BDM���ܳ����Ϊ____________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��a��b����������![]() ��һ���㣬OB��OA���������ڵ�B��c��d��������A�����������˶��Ĺ����У���A��������ԭ��O�غϣ������½��ۣ���acΪ��ֵ����ac=��bd���ۡ�AOB�����Ϊ��ֵ����ֱ��AB�ع�һ���㣮��ȷ���У�������
��һ���㣬OB��OA���������ڵ�B��c��d��������A�����������˶��Ĺ����У���A��������ԭ��O�غϣ������½��ۣ���acΪ��ֵ����ac=��bd���ۡ�AOB�����Ϊ��ֵ����ֱ��AB�ع�һ���㣮��ȷ���У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����Ƥ�����α�Ե��������״��MN=4�������߶��㴦����MN�ľ�����4��Ҫ����Ƥ�Ͻ���һ����ABCD��ʹ���ζ���B��C���ڱ�MN�ϣ�A��D�����������ϣ�
��1����ͼ�����ʵ�������ϵ���������߽���ʽ��
��2�������ABCD���ܳ�ΪL����C������Ϊ��m��0������L��m�Ĺ�ϵʽ����Ҫ��д�Ա���ȡֵ��Χ����
��3������������ȥ�ľ�����Ƥ���ܳ��ܷ����9.5����������9.5����˵�����ɣ�������9.5��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��b��c���dz�������ͼ���㣨1��0���ͣ�0��2����
��1������2��x��2ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m+n=1�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���֪AB=AC��AB�Ĵ�ֱƽ���߽�AB�ڵ�N����AC�ڵ�M������MB��
��1������ABC=70�������NMA�Ķ������� ���ȣ�
��2����AB=8cm����MBC���ܳ���14cm��
����BC�ij��ȣ�
������PΪֱ��MN��һ�㣬����ֱ��д����PBC�ܳ�����Сֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com