
����Ŀ����һ��ֱ�Ĺ�·����M��N���أ��׳���M��ʻ��N�أ��ٶ�Ϊ60km/h���ҳ���M��ʻ��N�أ��ٶ�Ϊ40km/h��������N��ʻ��M�أ��ٶ�Ϊ80km/h��������ͬʱ�������ȵ�Ŀ�ĵصij�ֹͣ������;�м׳��������ϣ�����ͣ��������2.5h���ú�������ԭ��ʻ��N�أ���׳���ʻ��ʱ��Ϊt��h�����ס�������֮��ľ���ΪS1��km�����ס���������M�صľ���ΪS2��km����S1��t֮��Ĺ�ϵ��ͼ1��ʾ��S2��t֮��Ĺ�ϵ��ͼ2��ʾ���������е���Ϣ�ش��������⣺

��1����ͼ1�е�C��ʵ���������� ����
�ڵ�B�ĺ��������� ������E�ĺ��������� ������Q���������� ����
��2�������ͼ2���߶�QR����ʾ��S2��t֮��Ĺ�ϵʽ��
��3�����ס���������70kmʱ����ֱ��д��t��ֵ��
���𰸡���1���پ���3Сʱ������������������1��3.75����3.5��60������2��y��60x��150����3��![]() ��4Сʱ
��4Сʱ
��������
��1���ٸ��������֪��C��ʵ�������Ǿ���3Сʱ���������������������������ʱ������ʻ��ʱ�䣬�����B���꣬�������D����Q���꣬��ͼ������E���꣬������⣻
��2���ô���ϵ�����������ʽ��
��3���ɼס���������70km������������г����̿���⣮
�⣺��1���١ߵ�C�����꣨3��0����
���CC��ʵ�������Ǿ���3Сʱ����������������
�ʴ�Ϊ������3Сʱ����������������
�������ʻxСʱ�׳��������ϣ�
������ɵ�60x+80��3��300
��x��1��
���B�ĺ�����Ϊ1��
���D�ĺ�����Ϊ3.5��
���Q������3.5��60��
��ͼ���֪����E��ʾ��������N�أ�
��t��![]() ��3.75h��
��3.75h��
���E�ĺ�����Ϊ3.75��
�ʴ�Ϊ��1��3.75����3.5��60��
��2�����߶�QR�ĺ�������ʽΪ��y��kx+b��
![]()
��ã�![]()
���߶�QR�ĺ�������ʽΪ��y��60x��150��
��3���辭��xСʱ���ס���������70km��
������ɵã�40x��60��70��40x��60��x��2.5����70
��x��![]() ��4��
��4��
��![]() ��4Сʱ���ס���������70km��
��4Сʱ���ס���������70km��


 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���ı���ABCD�У��Խ���BDƽ�֡�ABC����ACB��74������ABC��46�����ҡ�BAD+��CAD��180������ô��BDC�Ķ���Ϊ_____��
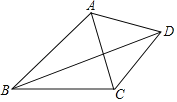
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ͼ1��ͼ2�е��ı���ABCD���������Σ���ABE�ı߳��ֱ�Ϊa��b��c�������ͼ1��ͼ2��ͼ2��ͼ3�ı任�����У����ü���ͼ�ε������ϵ����a��b��c֮��ĵ�����ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90�㣬AC=BC������ABC�����ֱ��CP����A����ֱ��CP�ĶԳƵ�ΪD������AD��BD������BD��ֱ��CP�ڵ�E��
��1����ͼ1����ACP=15�㣮
�������ⲹȫͼ�Σ�
�����CBD�Ķ�����
��2����ͼ2����45�㣼��ACP��90����ֱ���õ�ʽ��ʾ�߶�AC��DE��BE֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD�У�AB��3��BC��4����E��BC����һ�㣬����AE���ѡ�B��AE�۵���ʹ��B���ڵ�B����������CEB��Ϊֱ��������ʱ��BE�ij�Ϊ( )
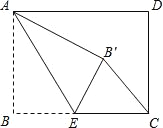
A. 3 B. ![]() C. 2��3 D. 3��
C. 2��3 D. 3��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c�Ķ�������Ϊ��2��9������y�ύ�ڵ�A��0��5������x�ύ�ڵ�E��B��
��1������κ���y=ax2+bx+c�ı���ʽ��
��2������A��ACƽ����x�ᣬ���������ڵ�C����PΪ�������ϵ�һ�㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D���ʵ���P�ں�λ��ʱ���ı���APCD�������������������
��3������M���������ϣ���N����Գ����ϣ�ʹ����A��E��N��MΪ������ı�����ƽ���ı��Σ���AEΪ��һ�ߣ����M��N�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ���ABC�У��߶�AMΪBC���ϵ����ߣ�����D��ֱ��AM��ʱ����CDΪһ����CD���·����ȱ���CDE������BE��
��1�����CAM�Ķ�����
��2������D���߶�AM��ʱ����֤����ADC����BEC��
��3������D��ֱ��AM��ʱ����ֱ��BE��ֱ��AM�Ľ���ΪO�����ж���AOB�Ƿ�Ϊ��ֵ����˵�����ɣ�
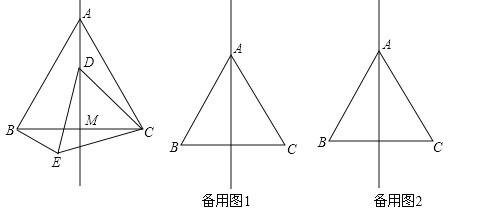
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҩ�����۲��Ÿ����г����н�����Ըó�������һ������ԭ��ҩδ����������۽���Ԥ�⣬����������ģ�ͣ����t���¸�ԭ��ҩ����������ΪP����λ���֣���P��t֮�������ͼ��ʾ�ĺ�����ϵ����ͼ���Ǻ���P=![]() ��0��t��8����ͼ�����߶�AB����ϣ����t�������۸�ԭ��ҩÿ�ֵ�ë����ΪQ����λ����Ԫ����Q��t֮���������¹�ϵ��Q=
��0��t��8����ͼ�����߶�AB����ϣ����t�������۸�ԭ��ҩÿ�ֵ�ë����ΪQ����λ����Ԫ����Q��t֮���������¹�ϵ��Q=![]()
��1����8��t��24ʱ����P����t�ĺ�������ʽ��
��2�����t�������۸�ԭ��ҩ����ë����Ϊw����λ����Ԫ��
����w����t�ĺ�������ʽ��
�ڸ�ҩ�����۲��ŷ�����Ϊ��336��w��513���������ڸ�ԭ��ҩ�ɳ������������۵���ë����Χ����˷�Χ����Ӧ����������P����Сֵ�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ξ�������ο���y�����ˣ�����Ʊ�۸�x��Ԫ����һ�κ������亯��ͼ������ͼ��
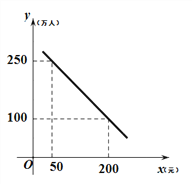
��1����y����x�ĺ�������ʽ��
��2���������㹤����Աͳ�Ʒ��֣�ÿ����һ����Ʊ����ɱ�Ϊ20Ԫ����ôҪ����������11500��Ԫ������Ʊ�۸ø���230Ԫ���������Ʊ�۸�Ӧ�ö�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com