
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c�Ķ�������Ϊ��2��9������y�ύ�ڵ�A��0��5������x�ύ�ڵ�E��B��
��1������κ���y=ax2+bx+c�ı���ʽ��
��2������A��ACƽ����x�ᣬ���������ڵ�C����PΪ�������ϵ�һ�㣨��P��AC�Ϸ�������PDƽ����y�ύAB�ڵ�D���ʵ���P�ں�λ��ʱ���ı���APCD�������������������
��3������M���������ϣ���N����Գ����ϣ�ʹ����A��E��N��MΪ������ı�����ƽ���ı��Σ���AEΪ��һ�ߣ����M��N�����꣮

���𰸡���1��y=��x2+4x+5����2����P��![]() ��
��![]() ��ʱ��S�ı���APCD���=
��ʱ��S�ı���APCD���=![]() ����3����M�������Ϊ��1��8��ʱ��N������Ϊ��2��13������M�������Ϊ��3��8��ʱ��N������Ϊ��2��3����
����3����M�������Ϊ��1��8��ʱ��N������Ϊ��2��13������M�������Ϊ��3��8��ʱ��N������Ϊ��2��3����
��������
���⣨1����������߽���ʽ���ô���ϵ������⼴�ɣ���2�������ֱ��AB����ʽ�������P���꣨x����x2+4x+5��������������ϵʽS�ı���APCD=��2x2+10x�����ݶ��κ��������ֵ����3�����жϳ���HMN�ա�AOE�����M��ĺ����꣬�Ӷ������M��N�����꣮
�����������1���������߽���ʽΪy=a![]() +9������������y�ύ�ڵ�A��0��5���� ��4a+9=5��
+9������������y�ύ�ڵ�A��0��5���� ��4a+9=5��
��a=��1�� y=��![]() +9=-
+9=-![]() +4x+5��
+4x+5��
��2����y=0ʱ��-![]() +4x+5=0����x1=��1��x2=5����E����1��0����B��5��0����
+4x+5=0����x1=��1��x2=5����E����1��0����B��5��0����
��ֱ��AB�Ľ���ʽΪy=mx+n����A��0��5����B��5��0������m=��1��n=5��
��ֱ��AB�Ľ���ʽΪy=��x+5����P��x����![]() +4x+5���� ��D��x����x+5����
+4x+5���� ��D��x����x+5����
��PD=-![]() +4x+5+x��5=-
+4x+5+x��5=-![]() +5x�� ��AC=4�� ��S�ı���APCD=
+5x�� ��AC=4�� ��S�ı���APCD=![]() ��AC��PD=2��-
��AC��PD=2��-![]() +5x��=-2
+5x��=-2![]() +10x��
+10x��
����x=![]() ʱ�� ��S�ı���APCD���=
ʱ�� ��S�ı���APCD���=![]() ��
��
��3����ͼ��
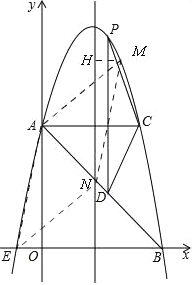
��M��MH��ֱ�ڶԳ��ᣬ����ΪH����MN��AE��MN=AE�����HMN�ա�AOE����HM=OE=1��
��M��ĺ�����Ϊx=3��x=1����x=1ʱ��M��������Ϊ8����x=3ʱ��M��������Ϊ8��
��M�������ΪM1��1��8����M2��3��8������A��0��5����E/span>����1��0���� ��ֱ��AE����ʽΪy=5x+5��
��MN��AE����MN�Ľ���ʽΪy=5x+b������N�������߶Գ���x=2�ϣ���N��2��10+b����
��AE2=OA2+0E2=26 ��MN=AE ��MN2=AE2�� ��MN2=��2��1��2+[8����10+b��]2=1+��b+2��2
��M�������ΪM1��1��8����M2��3��8���� ����M1��M2���������߶Գ���x=2�Գƣ�
����N�������߶Գ����ϣ� ��M1N=M2N�� ��1+��b+2��2=26�� ��b=3����b=��7��
��10+b=13��10+b=3 ����M�������Ϊ��1��8��ʱ��N������Ϊ��2��13����
��M�������Ϊ��3��8��ʱ��N������Ϊ��2��3����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�A����1��4����B����3��3����C����2��1��
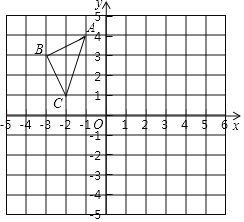
��1����֪��A��B��C������ABC����x��Գƣ�������A��B��C������д�����¸������꣺A���� ����B���� ����C���� ����
��2����y����������P����ͼ����ʾ��ͼ���̣���ʹ��PA+PC��ֵ��С����д����P�������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P���߶�MN��һ���㣬�ֱ���PM��PNΪһ�ߣ���MN��ͬ������APM����BPN��������BM��AN��

������ͼ1����PM��AP��PN��BP�ҡ�APM����BPN��90��ʱ���Բ���BM��AN֮���������ϵ��λ�ù�ϵ����֤����IJ��룻
������ͼ2������APM����BPN���ǵȱ�������ʱ��������BM��AN֮���������ϵ�Ƿ���Ȼ����������������֤����Ľ��ۣ�������������˵�����ɣ�
�����ڣ��������£�����AB�õ�ͼ3����PN��2PMʱ�����PAB������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC���ϵĸ�CE��BD�ཻ�ڵ�P��ͼ������BPE���Ƶ������ι��У�������
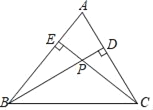
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ�Ĺ�·����M��N���أ��׳���M��ʻ��N�أ��ٶ�Ϊ60km/h���ҳ���M��ʻ��N�أ��ٶ�Ϊ40km/h��������N��ʻ��M�أ��ٶ�Ϊ80km/h��������ͬʱ�������ȵ�Ŀ�ĵصij�ֹͣ������;�м׳��������ϣ�����ͣ��������2.5h���ú�������ԭ��ʻ��N�أ���׳���ʻ��ʱ��Ϊt��h�����ס�������֮��ľ���ΪS1��km�����ס���������M�صľ���ΪS2��km����S1��t֮��Ĺ�ϵ��ͼ1��ʾ��S2��t֮��Ĺ�ϵ��ͼ2��ʾ���������е���Ϣ�ش��������⣺

��1����ͼ1�е�C��ʵ���������� ����
�ڵ�B�ĺ��������� ������E�ĺ��������� ������Q���������� ����
��2�������ͼ2���߶�QR����ʾ��S2��t֮��Ĺ�ϵʽ��
��3�����ס���������70kmʱ����ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ������ ��
A����һö���ȵ����ӣ�����ֹͣת����6�㳯���DZ�Ȼ�¼�
B���ס�����������ͬ�����¸����10�Σ����ǵijɼ�ƽ������ͬ������ֱ���![]() ��
��![]() ���������ɼ����ȶ�
���������ɼ����ȶ�
C�������콵��ĸ���Ϊ![]() ������ʾ�����а��춼�ڽ���
������ʾ�����а��춼�ڽ���
D���˽�һ�����ӻ���ʹ���������ʺ����ղ�ķ�ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̲ij��֣���ͼ�ǻ�ʦ����꼶�ϲ���ѧ�̲ĵ�96ҳ�IJ������ݣ�
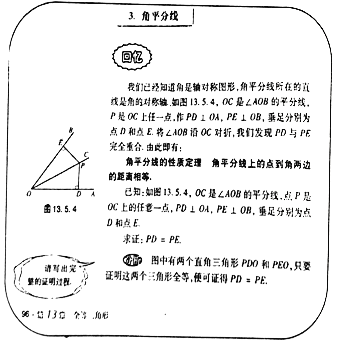

����ݽ̲��еķ��������ͼ�٣�д������ƽ���ߵ����ʶ�����������֤�����̣�
����Ӧ�ã�
��ͼ�ڣ����ı���ABCD�У���B����C����E�ڱ�BC�ϣ�AEƽ�֡�BAD��DEƽ�֡�ADC��
��1����֤��BE��CE��
��2�����ı���ABCD���ܳ�Ϊ24��BE��2�����Ϊ30�����ABE�ı�AB�ĸߵij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=x2��2x��3��x�ύ��A��B���㣬��y�ύ�ڵ�C���������ߵĶ���ΪM��
��1�����A��B��C�����꣮
��2����ֱ��BM�ĺ�������ʽ��
��3����˵������CBM+��CMB=90�㣮
��4�������������Ƿ���ڵ�P��ʹֱ��CP����BCM�ֳ������ȵ������֣������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
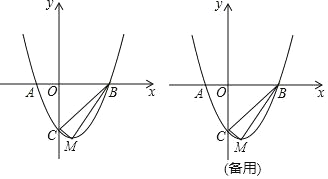
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ750��ְ�������μ���ƶ������ѧУ������Ϊ�˽�ְ���ľ�������������������ķ�����ȡ30��ְ����Ϊ�����������ǵľ���������ͳ�ƣ�ͳ�ƽ������4����5����6����7����8�����࣬�ֱ���A��B��C��D��E��ʾ������ͳ�����ݻ��Ƴ�����ͼ��ʾ�IJ�����������ͳ��ͼ����ͼ�и�������Ϣ����������⣺
��1����ȫ����ͳ��ͼ��
��2������30��ְ�����鱾����ƽ��������������λ����
��3�����Ƹõ�λ750��ְ����������ٱ���
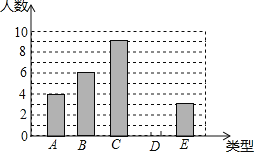
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com