
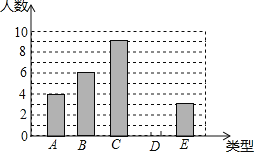
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
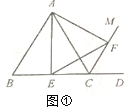
【题目】【感知】如图①,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC中点,在CM上截取CF=BE,连接AE、EF、AF.易证:△AEF是等边三角形(不需要证明).
【探究】如图②,△ABC是等边三角形,CM是外角∠ACD的平分线,E是边BC上一点(不与点B、C重合),在CM上截取CF=BE,连接AE、EF、AF.求证:△AEF是等边三角形.
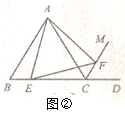
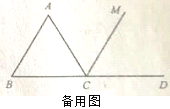
【应用】将图②中的“E是边BC上一点”改为“E是边BC延长线上一点”,其他条件不变.当四边形ACEF是轴对称图形,且AB=2时,请借助备用图,直接写出四边形ACEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励民众节约用电,城镇居民生活用电电费目前实行梯度收费,具体标准如下表:
月用电量(单位:千瓦时) | 单价(单位:元) |
150以内(含150) | 0.5 |
超过150但不超过300的部分(含300) | 0.6 |
300以上(不含300)的部分 | 0.8 |
(1)若月用电100千瓦时,应交电费多少元?若月用电200千瓦时,应交电费多少元?
(2)若某用户12月应交电费93元,该用户12月的用电量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B 两个码头相距800km,现有甲、乙两艘轮船分别以40km/h,60km/h 的速度从A、B 两地同时相向而行.已知轮船从A 码头开往B码头顺流航行.设水流的速度为a km/h,则:
(1)甲轮船在静水中的速度为__________km/h,乙轮船在静水中的速度为____________km/h;
(2)多少小时后甲、乙两艘轮船相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:在四边形中,一条边上的两个角称为邻角.如果一条边上的邻角相等,且这条边对边上的邻角也相等,则把这样的四边形叫做“完美四边形”.
初步运用:在“平行四边形、矩形和菱形”这三种特殊的四边形中,一定是“完美四边形”的是______;
问题探究:在完美四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求该完美四边形的周长与面积;
,求该完美四边形的周长与面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两桶水,甲桶装有![]() 升水,乙桶中的水比甲桶中的水多3升.现将甲桶中倒一半到乙桶中,然后再将此时乙桶中总水量的
升水,乙桶中的水比甲桶中的水多3升.现将甲桶中倒一半到乙桶中,然后再将此时乙桶中总水量的![]() 倒给甲桶,假定桶足够大,水不会溢岀.我们将上述两个步骤称为一次操作,进行重复操作,则( )
倒给甲桶,假定桶足够大,水不会溢岀.我们将上述两个步骤称为一次操作,进行重复操作,则( )
A. 每操作一次,甲桶中的水量都会减小,最后甲桶中的水会全部倒入乙桶
B. 每操作一次,甲桶中的水量都会减小,但永远倒不完
C. 每操作一次,甲桶中的水量都会增加,反复操作,最后甲桶中的水会比乙桶多
D. 每操作一次,甲桶中的水量都会增加,但永远比乙桶中的水量要少
查看答案和解析>>
科目:初中数学 来源: 题型:
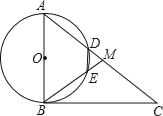
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.连结DE,使四边形DEBA为⊙O的内接四边形.
(1)求证:∠A=∠ABM=∠MDE;
(2)若AB=6,当AD=2DM时,求DE的长度;
(3)连接OD,OE,当∠A的度数为60°时,求证:四边形ODME是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com