【题目】如图所示，在平面直角坐标系中，A（﹣1，4），B（﹣3，3），C（﹣2，1）
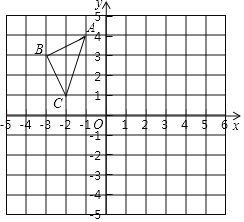
（1）已知△A′B′C′与△ABC关于x轴对称，画出△A′B′C′，并写出以下各点坐标：A′ ；B′ ；C′ ．
（2）在y轴上作出点P（在图中显示作图过程），使得PA+PC的值最小，并写出点P的坐标 ．
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，小李从市场上买回一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为35 m3的无盖长方体箱子，且此长方体箱子的底面长比宽多2m，现己知购买这种铁皮每平方米需30元钱，问小李购回这张矩形铁皮共花了多少元钱?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=﹣
x+c与x轴交于点A（3，0），与y轴交于点B，抛物线y=﹣
x2+bx+c经过点A，B．
（1）求点B的坐标和抛物线的解析式；
（2）M（m，0）为x轴上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．
①点M在线段OA上运动，若以B，P，N为顶点的三角形与△APM相似，求点M的坐标；
②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”．请直接写出使得M，P，N三点成为“共谐点”的m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
，
中，
，
，
，
，将绕着点
旋转一定的角度，得到
.
（1）若点
为
边上中点，连接
，则线段的范围为________.
（2）如图
，当直角顶点
在边上时，延长
，交
边于点
，请问线段、
、
具有怎样的数量关系，请写出探索过程．
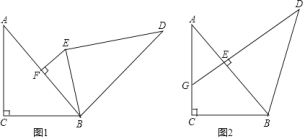
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：四边形ABCD中，对角线BD平分∠ABC，∠ACB＝74°，∠ABC＝46°，且∠BAD+∠CAD＝180°，那么∠BDC的度数为_____．
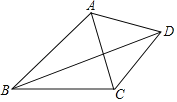
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知CF是△ABC的外角∠ACE的角平分线，D为CF上一点，且DA＝DB．
（1）求证：∠ACB＝∠ADB；
（2）求证：AC+BC＜2BD；
（3）如图2，若∠ECF＝60°，证明：AC＝BC+CD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
与
轴相交于
、
两点（其中为坐标原点），过点
作直线
轴于点
，交抛物线于点
，点关于抛物线对称轴的对称点为
（其中、不重合），连接
交
轴于点
，连接
和
．
（1）
时，求抛物线的解析式和的长；
如图
时，若
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，线段AB 是⊙O的直径，弦CD⊥AB于点H，点M是弧CBD 上任意一点，AH=2，CH=4．
（1）求⊙O 的半径r 的长度；
（2）求sin∠CMD；
（3）直线BM交直线CD于点E，直线MH交⊙O 于点 N，连接BN交CE于点 F，求HE
HF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c的顶点坐标为（2，9），与y轴交于点A（0，5），与x轴交于点E、B．
（1）求二次函数y=ax2+bx+c的表达式；
（2）过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积；
（3）若点M在抛物线上，点N在其对称轴上，使得以A、E、N、M为顶点的四边形是平行四边形，且AE为其一边，求点M、N的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
