
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(其中
两点(其中![]() 为坐标原点),过点
为坐标原点),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() (其中
(其中![]() 、
、![]() 不重合),连接
不重合),连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 和
和![]() .
.
(1)![]() 时,求抛物线的解析式和
时,求抛物线的解析式和![]() 的长;
的长;
![]() 如图
如图![]() 时,若
时,若![]() ,求
,求![]() 的值.
的值.

【答案】![]()
![]() ,∴
,∴![]() ;
;![]()
![]() .
.
【解析】
(1)令a=![]() 代入抛物线,由于抛物线过原点,所以b=0,从而求出抛物线的解析式,然后根据条件求出点B与C的坐标即可求出BC的长度.
代入抛物线,由于抛物线过原点,所以b=0,从而求出抛物线的解析式,然后根据条件求出点B与C的坐标即可求出BC的长度.
(2)由题意可知b=0,然后根据P的坐标分别求出A、B、C、M的坐标,进而求出BC、BP、PM、AM的长度,最后利用△AMP∽△BPC列出关于a的方程即可求出a的值.
![]() 当
当![]() 时,
时,
∴抛物线为:![]() ,
,
∴对称轴为![]() ,
,
又∵抛物线过原点,
∴![]() ,
,
∴![]() ,
,
∴令![]() 代入
代入![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() 由于抛物线过原点
由于抛物线过原点![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() 代入
代入![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∵点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,
,
抛物线的对称轴为![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1与l2相交,且夹角为45°,点P在角的内部,小明用下面的方法作点P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作点P1关于l2的对称点P2,然后再以l1为对称轴作点P2关于l1的对称点P3,以l2为对称轴作点P3关于l2的对称点P4,...,如此继续,得到一系列的点P1,P2,...,Pn,若点Pn与点P重合,则n的值可以是( )

A.2019B.2018C.2017D.2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD.
AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD.
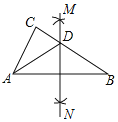
(1)根据作图判断:△ABD的形状是 ;
(2)若BD=10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(﹣1,4),B(﹣3,3),C(﹣2,1)
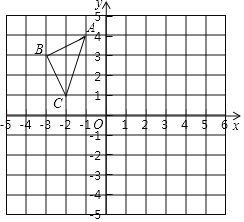
(1)已知△A′B′C′与△ABC关于x轴对称,画出△A′B′C′,并写出以下各点坐标:A′ ;B′ ;C′ .
(2)在y轴上作出点P(在图中显示作图过程),使得PA+PC的值最小,并写出点P的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:
![]() 将函数关系式用配方法化为
将函数关系式用配方法化为![]() 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
![]() 在直角坐标系中,画出它的图象.
在直角坐标系中,画出它的图象.
![]() 根据图象说明:当
根据图象说明:当![]() 取何值时,
取何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 当
当![]() 取何值时,
取何值时,![]() ?
?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为维护南海主权,我海军舰艇加强对南海海域的巡航,![]() 年
年![]() 月
月![]() 日上午
日上午![]() 时,我海巡
时,我海巡![]() 号舰艇在观察点
号舰艇在观察点![]() 处观测到其正东方向
处观测到其正东方向![]() 海里处有一灯塔
海里处有一灯塔![]() ,该舰艇沿南偏东
,该舰艇沿南偏东![]() 的方向航行,
的方向航行,![]() 时到达观察点
时到达观察点![]() ,测得灯塔
,测得灯塔![]() 位于其北偏西
位于其北偏西![]() 方向,求该舰艇的巡航速度?(结果保留整数)
方向,求该舰艇的巡航速度?(结果保留整数)
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=
x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=![]() x+3上,若N点在第二象限内,则tan∠AON的值为( )
x+3上,若N点在第二象限内,则tan∠AON的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P是线段MN上一动点,分别以PM,PN为一边,在MN的同侧作△APM,△BPN,并连接BM,AN.

(Ⅰ)如图1,当PM=AP,PN=BP且∠APM=∠BPN=90°时,试猜想BM,AN之间的数量关系与位置关系,并证明你的猜想;
(Ⅱ)如图2,当△APM,△BPN都是等边三角形时,(Ⅰ)中BM,AN之间的数量关系是否仍然成立?若成立,请证明你的结论;若不成立,试说明理由.
(Ⅲ)在(Ⅱ)的条件下,连接AB得到图3,当PN=2PM时,求∠PAB度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
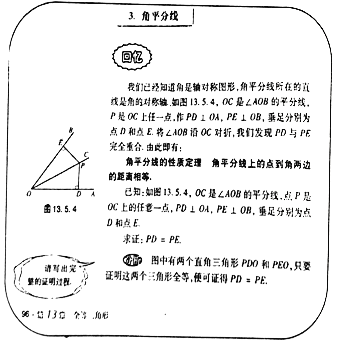

请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com