
【题目】为维护南海主权,我海军舰艇加强对南海海域的巡航,![]() 年
年![]() 月
月![]() 日上午
日上午![]() 时,我海巡
时,我海巡![]() 号舰艇在观察点
号舰艇在观察点![]() 处观测到其正东方向
处观测到其正东方向![]() 海里处有一灯塔
海里处有一灯塔![]() ,该舰艇沿南偏东
,该舰艇沿南偏东![]() 的方向航行,
的方向航行,![]() 时到达观察点
时到达观察点![]() ,测得灯塔
,测得灯塔![]() 位于其北偏西
位于其北偏西![]() 方向,求该舰艇的巡航速度?(结果保留整数)
方向,求该舰艇的巡航速度?(结果保留整数)
(参考数据:![]() ,
,![]() )
)

【答案】该舰艇的巡航速度约为![]() 海里/时.
海里/时.
【解析】
过点S作SC⊥AB,C为垂足.先解Rt△ACS,由∠CAS=45°,AS=80![]() ,得出SC=AC=80.再解Rt△BCS,由∠CBS=45°-15°=30°,得出BC=80
,得出SC=AC=80.再解Rt△BCS,由∠CBS=45°-15°=30°,得出BC=80![]() ,那么AB=AC+BC=80+80
,那么AB=AC+BC=80+80![]() ,然后根据速度=路程÷时间即可求出该舰艇的巡航速度.
,然后根据速度=路程÷时间即可求出该舰艇的巡航速度.
过点S作SC⊥AB,C为垂足,
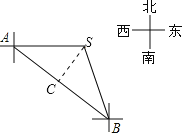
∵在Rt△ACS中,∠CAS=45°,AS=80![]() ,
,
∴SC=AC=80,
∵在Rt△BCS中,∠CBS=45°-15°=30°,
∴BC=80![]() ,
,
∴AB=AC+BC=80+80![]() ,
,
∴该舰艇的巡航速度是(80+80![]() )÷(11-9)=40+40
)÷(11-9)=40+40![]() ≈109(海里/时).
≈109(海里/时).
答:该舰艇的巡航速度约为109海里/时.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
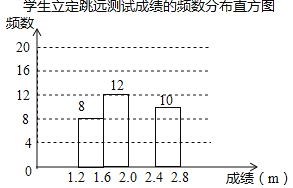
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕着点
绕着点![]() 旋转一定的角度,得到
旋转一定的角度,得到![]() .
.
(1)若点![]() 为
为![]() 边上中点,连接
边上中点,连接![]() ,则线段
,则线段![]() 的范围为________.
的范围为________.
(2)如图![]() ,当
,当![]() 直角顶点
直角顶点![]() 在
在![]() 边上时,延长
边上时,延长![]() ,交
,交![]() 边于点
边于点![]() ,请问线段
,请问线段![]() 、
、![]() 、
、![]() 具有怎样的数量关系,请写出探索过程.
具有怎样的数量关系,请写出探索过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
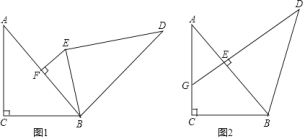
【题目】如图1,已知CF是△ABC的外角∠ACE的角平分线,D为CF上一点,且DA=DB.

(1)求证:∠ACB=∠ADB;
(2)求证:AC+BC<2BD;
(3)如图2,若∠ECF=60°,证明:AC=BC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(其中
两点(其中![]() 为坐标原点),过点
为坐标原点),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,点
,点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() (其中
(其中![]() 、
、![]() 不重合),连接
不重合),连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() 和
和![]() .
.
(1)![]() 时,求抛物线的解析式和
时,求抛物线的解析式和![]() 的长;
的长;
![]() 如图
如图![]() 时,若
时,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB 是⊙O的直径,弦CD⊥AB于点H,点M是弧CBD 上任意一点,AH=2,CH=4.
(1)求⊙O 的半径r 的长度;
(2)求sin∠CMD;
(3)直线BM交直线CD于点E,直线MH交⊙O 于点 N,连接BN交CE于点 F,求HE![]() HF的值.
HF的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD,AB=AC,E、F分别是BC,AD的中点,连接AE、CF.
(1)求证:四边形AECF是矩形;
(2)若AB=2,求菱形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,点D在线段AC上,且CD=7cm,动点P从距B点15cm的E点出发,以每秒2cm的速度沿射线EA的方向运动,时间为t秒.
(1)求AD的长.
(2)用含有t的代数式表示AP的长.
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.
(4)直接写出t=______秒时,△PBC为等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com