
【题目】如图1,已知CF是△ABC的外角∠ACE的角平分线,D为CF上一点,且DA=DB.

(1)求证:∠ACB=∠ADB;
(2)求证:AC+BC<2BD;
(3)如图2,若∠ECF=60°,证明:AC=BC+CD.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)过点D分别作AC,CE的垂线,垂足分别为M,N,证明Rt△DAM≌Rt△DBN,得出∠DAM=∠DBN,则结论得证;
(2)证明Rt△DMC≌Rt△DNC,可得CM=CN,得出AC+BC=2BN,又BN<BD,则结论得证;
(3)在AC上取一点P,使CP=CD,连接DP,可证明△ADP≌△BDC,得出AP=BC,则结论可得出.
(1)证明:过点D分别作AC,CE的垂线,垂足分别为M,N,
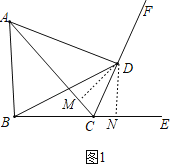
∵CF是△ABC的外角∠ACE的角平分线,
∴DM=DN,
在Rt△DAM和Rt△DBN中,
![]() ,
,
∴Rt△DAM≌Rt△DBN(HL),
∴∠DAM=∠DBN,
∴∠ACB=∠ADB;
(2)证明:由(1)知DM=DN,
在Rt△DMC和Rt△DNC中,
![]() ,
,
∴Rt△DMC≌Rt△DNC(HL),
∴CM=CN,
∴AC+BC=AM+CM+BC=AM+CN+BC=AM+BN,
又∵AM=BN,
∴AC+BC=2BN,
∵BN<BD,
∴AC+BC<2BD.
(3)由(1)知∠CAD=∠CBD,在AC上取一点P,使CP=CD,
连接DP,
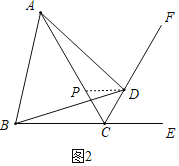
∵∠ECF=60°,∠ACF=60°,
∴△CDP为等边三角形,
∴DP=DC,∠DPC=60°,
∴∠APD=120°,
∵∠ECF=60°,
∴∠BCD=120°,
在△ADP和△BDC中,
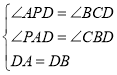 ,
,
∴△ADP≌△BDC(AAS),
∴AP=BC,
∵AC=AP+CP,
∴AC=BC+CP,
∴AC=BC+CD.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】在等边△ABC中.
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、正方形A3B3C3C2、…、正方形AnBnnCn﹣1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则△A2018A2019B2018的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块长方形纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=2cm,则BC的长度为( )cm.
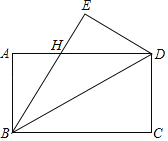
A.8B.7C.6D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(﹣1,4),B(﹣3,3),C(﹣2,1)
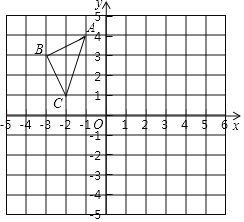
(1)已知△A′B′C′与△ABC关于x轴对称,画出△A′B′C′,并写出以下各点坐标:A′ ;B′ ;C′ .
(2)在y轴上作出点P(在图中显示作图过程),使得PA+PC的值最小,并写出点P的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标系中一条圆弧经过正方形网格的格点![]() 、
、![]() 、
、![]() .若
.若![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
![]() 圆弧所在圆的圆心
圆弧所在圆的圆心![]() 点的坐标为________
点的坐标为________
![]() 点
点![]() 是否在经过点
是否在经过点![]() 、
、![]() 、
、![]() 三点的抛物线上;
三点的抛物线上;
![]() 在
在![]() 的条件下,求证:直线
的条件下,求证:直线![]() 是
是![]() 的切线.
的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为维护南海主权,我海军舰艇加强对南海海域的巡航,![]() 年
年![]() 月
月![]() 日上午
日上午![]() 时,我海巡
时,我海巡![]() 号舰艇在观察点
号舰艇在观察点![]() 处观测到其正东方向
处观测到其正东方向![]() 海里处有一灯塔
海里处有一灯塔![]() ,该舰艇沿南偏东
,该舰艇沿南偏东![]() 的方向航行,
的方向航行,![]() 时到达观察点
时到达观察点![]() ,测得灯塔
,测得灯塔![]() 位于其北偏西
位于其北偏西![]() 方向,求该舰艇的巡航速度?(结果保留整数)
方向,求该舰艇的巡航速度?(结果保留整数)
(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B.甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
C.“明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com